Đề bài
Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng \({\sin ^2}\alpha = {\sin ^2}\beta + {\sin ^2}\gamma \)
Phương pháp giải - Xem chi tiết
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Lời giải chi tiết
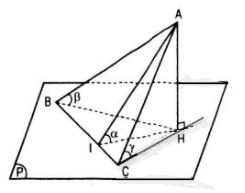
Kẻ AH ⊥ mp(P) và AI ⊥ BC.
Khi đó HB là hình chiếu của AB trên (P) nên góc giữa AB và (P) bằng góc giữa AB và HB hay \(\beta = \widehat {ABH}\)
HC là hình chiếu của AC trên (P) nên góc giữa AC và (P) bằng góc giữa AC và HC hay \(\gamma = \widehat {ACH}\)
Lại có:
\(\left\{ \begin{array}{l}
AI \bot BC\\
AH \bot BC\left( {AH \bot \left( P \right)} \right)
\end{array} \right. \) \(\Rightarrow BC \bot \left( {AIH} \right) \Rightarrow BC \bot HI\)
Mà \(BC \bot AI\) và \(\left( {ABC} \right) \cap \left( P \right) = BC\) nên góc giữa (ABC) và (P) bằng góc giữa AI và HI hay \(\alpha = \widehat {AIH}.\) (do \(\widehat {AIH}<90^0\)).
Vì ΔABC vuông ở A nên :
\(\eqalign{ & {1 \over {A{I^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}} \cr & \Rightarrow {{A{H^2}} \over {A{I^2}}} = {{A{H^2}} \over {A{B^2}}} + {{A{H^2}} \over {A{C^2}}} \cr & hay\,\,{\sin ^2}\alpha = {\sin ^2}\beta + {\sin ^2}\gamma \cr} \)

