Đề bài
Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’.
a. Chứng minh rằng đường thẳng CB’ song song với mp(AHC’)
b. Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (A’BC). Chứng minh rằng d song song với mp(BB’C’C)
c. Xác định thiết diện của hình lăng trụ ABC.A’B’C’khi cắt bởi mp(H , d)
Lời giải chi tiết
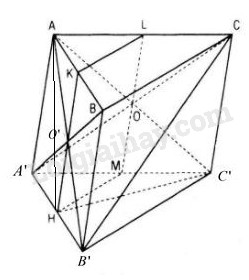
a) Chứng minh CB' // (AHC’)
Ta tìm trong (AHC’) một đường thẳng song song với CB’, muốn vậy ta tìm giao tuyến của (AHC’) với một mặt phẳng chứa CB’ và giao tuyến đó phải song song CB', đó là (A’B’C).
Dễ thấy \(H \in \left( {AHC'} \right) \cap \left( {A'B'C} \right)\)
Gọi O là giao điểm AC’ và A’C nên
\(\left\{ \begin{array}{l}
O \in AC' \subset \left( {AHC'} \right)\\
O \in A'C \subset \left( {A'B'C} \right)
\end{array} \right. \)\(\Rightarrow O \in \left( {AHC'} \right) \cap \left( {A'B'C} \right)\)
Do đó \(OH = \left( {AHC'} \right) \cap \left( {A'B'C} \right)\)
AA’C’C là hình bình hành nên O là trung điểm của A’C.
Do đó HO là đường trung bình của ∆A’B’C
⇒ HO // B’C ⇒ B’C // (AHC’).
(vì HO \(\subset\) (AHC’)).
b) Tìm giao tuyến d của (AB’C’) và (A’BC).
Gọi O’ là giao điểm của AB’ và A’B thì O, O’ là hai điểm chung của hai mặt phẳng (AB’C’) và (A’BC) nên (AB’C’) ∩ (A’BC) = OO’
Vậy d = OO’. Ta có O’ là trung điểm của AB’ ( vì AA’B’B là hình bình hành).
⇒ OO’ là đường trung bình của ∆AB’C’.
⇒ OO’ // B’C' // BC ⇒ OO’ // (BB’C’C) ⇒ d // (BB’C’C)
c) Gọi {K} = HO’ ∩ AB thì HK // AA’
Qua O kẻ ML // AA’ ( M ∈ A’C’, L ∈ AC).
Thiết diện cần tìm là hình bình hành HKLM.

