Cho hình tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc.
LG a
Chứng minh tam giác ABC có ba góc nhọn.
Lời giải chi tiết:
Đặt a = OA, b = OB, c = OC. Ta có:
\(AB = \sqrt {{a^2} + {b^2}} ,BC = \sqrt {{b^2} + {c^2}} ,\) \(AC = \sqrt {{a^2} + {c^2}} \)
Áp dụng định lí cosin trong tam giác ABC ta có :
\(\cos A = {{A{B^2} + A{C^2} - B{C^2}} \over {2AB.AC}} \) \( = {{{a^2} + {b^2} + {a^2} + {c^2} - {b^2} - {c^2}} \over {2AB.AC}} = {{2{a^2}} \over {2AB.AC}} > 0\)
⇒ A nhọn. Tương tự B, C là các góc nhọn.
Vậy ΔABC có ba góc nhọn.
LG b
Chứng minh rằng hình chiếu H của điểm O trên mp(ABC) trùng với trực tâm tam giác ABC.
Lời giải chi tiết:
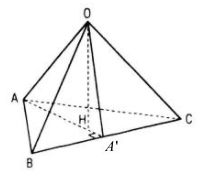

LG c
Chứng minh rằng \({1 \over {O{H^2}}} = {1 \over {O{A^2}}} + {1 \over {O{B^2}}} + {1 \over {O{C^2}}}\)
Lời giải chi tiết:


