Đề bài
Cho vecto →u và điểm O. Với điểm M bất kì, ta gọi M1là điểm đối xứng với M qua O và M’ là điểm sao cho →M1M′=→u. Gọi F là phép biến hình biến M thành M’
a. F là phép hợp thành của hai phép nào ? F có phải là phép dời hình hay không?
b. Chứng tỏ rằng F là một phép đối xứng tâm
Lời giải chi tiết
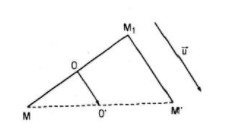
a. F là hợp thành của hai phép: phép đối xứng tâm ĐOvới tâm O và phép tịnh tiến T theo vecto →u. Ta có F là phép dời hình vì ĐO và T là phép dời hình
b. Giả sử M1 = ĐO(M) và M’ = T→u(M1)
Nếu gọi O’ là trung điểm của MM’ thì:
→OO′=→M1M′2=→u2
Vậy điểm O’ cố định và F chính là phép đối xứng qua tâm O’
