Đề bài
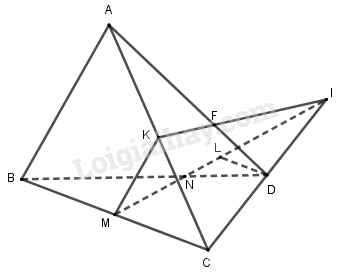
Cho tứ diện ABCD. Gọi M, K lần lượt là trung điểm của BC và AC, N là điểm trên cạnh BD sao cho BN = 2ND. Gọi F là giao điểm của AD và mp(MNK). Trong các mệnh đề sau đây, mệnh đề nào đúng ?
A. AF = FD B. AF = 2FD
C. AF = 3FD D. FD = 2AF
Phương pháp giải - Xem chi tiết
- Xác định giao điểm \(I\) (tìm một đường thẳng thuộc mặt phẳng \((KMN)\) mà cắt với \(AD\).
- Qua \(D\) kẻ đường thẳng song song với \(BC\), chứng minh \(D\) là trung điểm của \(CI\).
- Từ đó suy ra điều phải chứng minh.
Lời giải chi tiết
Trong mp\(\left( {BCD} \right)\), gọi \(I = MN \cap CD\) \( \Rightarrow I \in CD \subset \left( {ACD} \right)\).
Trong mp\(\left( {ACD} \right)\), gọi \(F = KI \cap AD\) \( \Rightarrow F \in AD,F \in KI \subset \left( {KMN} \right)\).
Vậy \(F = AD \cap \left( {KMN} \right)\).
Kẻ DL // BC (L ϵ MI)
\({{DL} \over {BM}} = {{DN} \over {BN}} = {1 \over 2} \Rightarrow DL = {1 \over 2}BM\) \(\Rightarrow DL = {1 \over 2}CM\) (do \(BM=CM\)).
Mà \(DL//CM \Rightarrow \dfrac{{DI}}{{CI}} = \dfrac{{DL}}{{CM}} = \dfrac{1}{2}\)
⇒ D là trung điểm CI.
Từ đó suy ra F là trọng tâm ΔACI nên AF = 2FD.
Chọn (B)