Đề bài
Chứng minh rẳng tổng bình phương tất cả các đường chéo của một hình hộp bằng tổng bình phương tất cả các cạnh của hình hộp đó
Phương pháp giải - Xem chi tiết
Áp dụng tính chất: “ Trong một hình bình hành, tổng bình phương hai đường chéo bằng tổng bình phương bốn cạnh.”
Chứng minh:
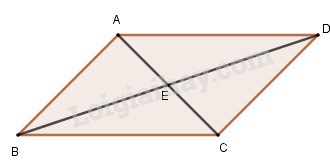
Ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC\cos B\\B{D^2} = A{B^2} + A{D^2} - 2AB.AD\cos A\\\,\,\,\,\,\,\,\,\,\,\, = A{B^2} + B{C^2} + 2AB.BC\cos B\end{array}\)
Vì \(AD = BC\) và \(\cos A = - \cos B\) (hai góc bù nhau thì cos đối nhau)
\( \Rightarrow A{C^2} + B{D^2} = 2A{B^2} + 2B{C^2}\) \( = 2\left( {A{B^2} + B{C^2}} \right)\).
Lời giải chi tiết
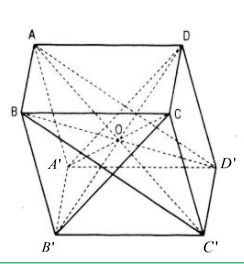
Đặt AB = a, BC = b, AA’ = c ( đó là 3 kích thước của hình hộp).
Trong hình bình hành ABC’D’ ta có:
\(AC'{^2} + BD{'^2} = 2\left( {{a^2} + BC'{^2}} \right)\) (1)
Trong hình bình hành A’B’CD ta có:
\(A'{C^2} + B'{D^2} = 2\left( {{a^2} + B'{C^2}} \right)\) (2)
Cộng (1) và (2) ta được :
\(AC'{^2} + BD'{^2}+A'{C^2} + B'{D^2} \)\(= 2\left( {2{a^2} + BC{'^2} + B'{C^2}} \right)\) (3)
Mặt khác trong hình bình hành BB’C’C ta có:
\(BC{'^2} + B'{C^2} = 2\left( {{b^2} + {c^2}} \right)\) (4)
Thay (4) vào (3) ta được :
\(AC'{^2} + BD'{^2} + A'{C^2} + B\,'{D^2}\)\( = 4\left( {{a^2} + {b^2} + {c^2}} \right)\) (đpcm).

