Đề bài
Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k,k \ne 0\)cho trước
Lời giải chi tiết
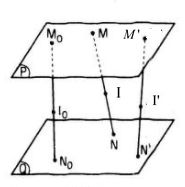
Thuận. Giả sử M \(\in\) (P), N \(\in\) (Q) và điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k.\)
Trên hai mặt phẳng (P) và (Q), ta lần lượt lấy hai điểm cố định M0 và N0 rồi lấy một điểm I0 thuộc đoạn thẳng M0N0 sao cho \({{{M_0}{I_0}} \over {{N_0}{I_0}}} = k.\) Khi ấy điểm I0 cố định.
Ta có: \({{IM} \over {IN}} = {{{I_0}{M_0}} \over {{I_0}{N_0}}}\left( { = k} \right)\)
\(\Rightarrow {{IM} \over {{I_0}{M_0}}} = {{IN} \over {{I_0}{N_0}}} = {{IM + IN} \over {{I_0}{M_0} + {I_0}{N_0}}} = {{MN} \over {{M_0}{N_0}}}\)
Áp dụng định lí Ta-lét đảo, ta suy ra đường thẳng I0I thuộc một mặt phẳng (R) song song với (P) và (Q).
Mặt phẳng (R) cố định vì nó qua điểm cố định I0 và song song với mặt phẳng cố định (P).
Vậy điểm I thuộc mặt phẳng (R) cố định.
Đảo. Ngược lại, lấy một điểm I’ bất kì trên mặt phẳng (R).
Qua I’ ta kẻ một đường thẳng cắt hai mặt phẳng (P) và (Q) lần lượt tại M’ và N’.
Xét hai cát tuyến M0N0 , M’N’ và ba mặt phẳng song song (P), (Q), (R).
Theo định lí Ta-lét ta có: \({{I'M'} \over {{I_0}{M_0}}} = {{I'N'} \over {{I_0}{N_0}}} = {{M'N'} \over {{M_0}{N_0}}}\)
Từ đó, ta suy ra I' thuộc đoạn thẳng M’N’ và \({{I'M'} \over {I'N'}} = {{{I_0}{M_0}} \over {{I_0}{N_0}}} = k\)
Kết luận: Tập hợp điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k\) là mặt phẳng (R) nói trên.

