Đề bài
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
Lời giải chi tiết
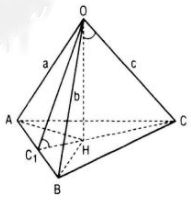
Vì OA, OB, OC đôi một vuông góc và H là hình chiếu của O trên mp(ABC) nên H là trực tâm tam giác ABC. Từ đó HC1 ⊥ AB (C1 là giao điểm của CH và AB), suy ra OC1 ⊥ AB. Như vậy ^OC1H là góc giữa mp(OAB) và mp(ABC).
Ta có: SHAB=SOABcos^OC1H
Mà ^OC1H=^HOC nên SHAB=SOABcos^HOC.
Ta lại có : cos^HOC=OHOC,1OH2=1OA2+1OB2+1OC2
Từ đó : cos^HOC=ab√a2b2+b2c2+c2a2
Mặt khác SOAB=12ab
Vậy SHAB=a2b22√a2b2+b2c2+c2a2
Tương tự như trên, ta có :
SHBC=b2c22√a2b2+b2c2+c2a2SHAC=c2a22√a2b2+b2c2+c2a2

