Đề bài
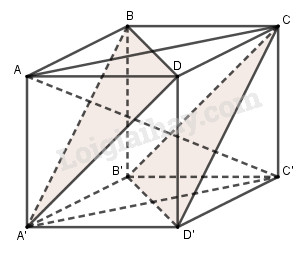
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a.
a. Chứng minh rằng AC’ vuông góc với hai mặt phẳng (A’BD) và (B’CD’).
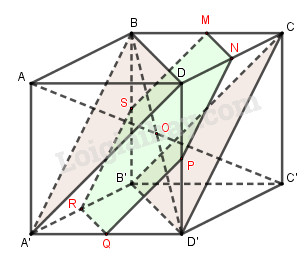
b. Cắt hình lập phương bởi mặt phẳng trung trực của AC’. Chứng minh thiết diện tạo thành là một lục giác đều. Tính diện tích thiết diện đó.
Lời giải chi tiết
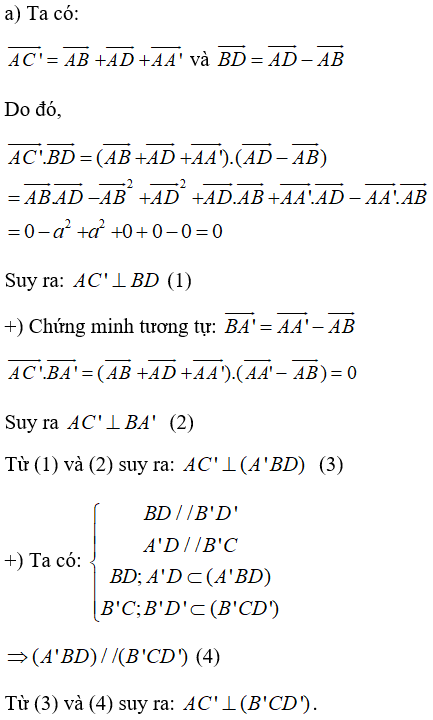
Cách khác:
Ta có: \(BD \bot AC\) (do \(ABCD\) là hình vuông)
\(BD \bot AA'\) (do \(AA' \bot \left( {ABCD} \right)\))
\( \Rightarrow BD \bot \left( {ACC'A'} \right)\) \( \Rightarrow BD \bot AC'\)
\(\left\{ \begin{array}{l}A'D \bot AD'\\A'D \bot AB\end{array} \right. \Rightarrow A'D \bot \left( {ABC'D'} \right)\)
\( \Rightarrow A'D \bot AC'\)
Ta có: \(\left\{ \begin{array}{l}BD \bot AC'\\A'D \bot AC'\end{array} \right.\) \( \Rightarrow AC' \bot \left( {A'BD} \right)\)
Lại có, \(\left\{ \begin{array}{l}BD//B'D'\\A'B//CD'\\BD,A'B \subset \left( {A'BD} \right)\\B'D',CD' \subset \left( {CB'D'} \right)\end{array} \right.\) \( \Rightarrow \left( {A'BD} \right)//\left( {CB'D'} \right)\)
\( \Rightarrow AC' \bot \left( {CB'D'} \right)\)
Vậy \(AC'\) vuông góc với các mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {CB'D'} \right)\).
b)
Gọi \(O\) là trung điểm của \(AC'\).
\(\left( P \right)\) là mặt phẳng trung trực của \(AC'\) thì \(\left( P \right)\) đi qua \(O\) và vuông góc với \(AC'\).
Mà \(AC'//\left( {A'BD} \right)\) và \(AC' \bot \left( {CB'D'} \right)\) nên \(\left( P \right)//\left( {A'BD} \right)//\left( {CB'D'} \right)\).
Ta có: \(\left\{ \begin{array}{l}BD \subset \left( {BDD'B'} \right)\\BD//\left( P \right)\\O \in \left( P \right) \cap \left( {BDD'B'} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {BDD'B'} \right) = Ot//BD\)
Trong \(\left( {BDD'B'} \right)\), qua \(O\) kẻ đường thẳng \(Ot//BD\) và cắt \(BB',DD'\) lần lượt tại các điểm \(S,P\).
Tương tự,
\(\left\{ \begin{array}{l}A'D \subset \left( {ADD'A'} \right)\\A'D//\left( P \right)\\P \in \left( P \right) \cap \left( {ADD'A'} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {ADD'A'} \right) = PQ//A'D\) với \(Q \in A'D\).
\(\left\{ \begin{array}{l}B'D \subset \left( {A'B'C'D'} \right)\\B'D//\left( P \right)\\Q \in \left( P \right) \cap \left( {A'B'C'D'} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {A'B'C'D'} \right) = QR//B'D'\) với \(R \in A'B'\).
\(\left\{ \begin{array}{l}CD' \subset \left( {CDD'C'} \right)\\CD'//\left( P \right)\\P \in \left( P \right) \cap \left( {CDD'C'} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {CDD'C'} \right) = PN//CD'\) với \(N \in CD\).
\(\left\{ \begin{array}{l}BD \subset \left( {ABCD} \right)\\BD//\left( P \right)\\N \in \left( P \right) \cap \left( {ABCD} \right)\end{array} \right.\) \( \Rightarrow \left( P \right) \cap \left( {ABCD} \right) = NM//BD\) với \(M \in BC\).
Vậy thiết diện là lục giác \(MNPQRS\).
Dễ thấy, \(O\) là trung điểm của \(AC'\) nên cũng là trung điểm của \(BD'\).
\( \Rightarrow PS//BD\) thì \(P,S\) lần lượt là trung điểm của \(DD',BB'\).
Từ đó các điểm \(M,N,Q,R\) lần lượt là trung điểm của \(BC,CD,D'A',A'B'\).
\(ABCD\) là hình vuông cạnh \(a\) nên \(BD = \sqrt {A{B^2} + A{D^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow MN = \frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\)
Tương tự \(MN = NP = PQ\) \( = QR = RS = SM = \frac{{a\sqrt 2 }}{2}\).
Do đó, lục giác \(MNPQRS\) là lục giác đều.
Xét \(\Delta MON\) đều cạnh \(OM = ON = MN = \frac{{a\sqrt 2 }}{2}\) nên có diện tích:
\({S_{MON}} = \frac{1}{2}OM.ON.\sin \widehat {MON}\) \( = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 2 }}{2}.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{8}\)
Vậy \({S_{MNPQRS}} = 6{S_{MON}}\) \( = 6.\frac{{{a^2}\sqrt 3 }}{8} = \frac{{3{a^2}\sqrt 3 }}{4}\).