Đề bài
Cho hình hộp ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Nếu
\(AC' = BD' = B'D = \sqrt {{a^2} + {b^2} + {c^2}} \)
Thì hình hộp đó có phải là hình hộp chữ nhật không ? Vì sao ?
Lời giải chi tiết
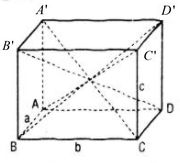
Áp dụng tính chất : “Tổng bình phương hai đường chéo hình bình hành bằng tổng bình phương bốn cạnh của nó” (BT 38, 4 chương II).
Ta có:
\(\eqalign{ & AC{'^2} + A'{C^2} = 2\left( {AA{'^2} + A'{C^2}} \right) \cr & B'{D^2} + BD{'^2} = 2\left( {BB{'^2} + B{D^2}} \right) \cr & \Rightarrow AC{'^2} + A'{C^2} + BD{'^2} + B'{D^2} \cr&\;\;\;= 2\left( {{c^2} + {c^2} + A{C^2} + B{D^2}} \right) = 4\left( {{a^2} + {b^2} + {c^2}} \right) \cr & \Rightarrow A'C = AC' = B'D = BD' \cr} \)
⇒ AA’C’C và BB’D’D là các hình chữ nhật .
Từ đó suy ra AA’ ⊥ AC và AA’ ⊥ BD. Do đó AA’ ⊥ (ABCD), tức hình hộp ABCD.A’B’C’D’là hình hộp chữ nhật.

