Xác định tâm vị tự trong và tâm vị tự ngoài của hai đường tròn trong các trường hợp sau :
LG a
Hai đường tròn tiếp xúc ngoài với nhau
Phương pháp giải:
Cách xác định tâm vị tự:
- Lấy điểm \(M\) thuộc đường tròn \((O)\).
- Qua \(O'\) kẻ đường thẳng song song với \(OM\), đường thẳng này cắt đường tròn \((O')\) tại \(M'\) và \(M''\).
- Hai đường thẳng \(MM'\) và \(MM''\) cắt đường thẳng \(OO'\) theo thứ tự \(I\) và \(I'\).
Khi đó, \(I\) và \(I'\) là các tâm vị tự cần tìm.
Lời giải chi tiết:
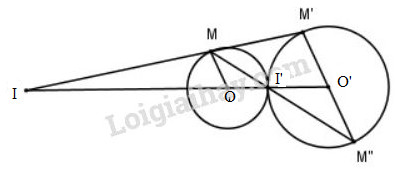
Gọi I là tâm vị tự ngoài, I’ là tâm vị tự trong của hai đường tròn \((O)\) và \((O’)\)
Nếu \((O)\) và \((O’)\) tiếp xúc ngoài thì tiếp điểm I’ là tâm vị tự trong, giao điểm của OO’ với tiếp tuyến chung ngoài của \((O)\) và \((O’)\) (nếu có) là tâm vị tự ngoài (h.a)
LG b
Hai đường tròn tiếp xúc trong với nhau
Lời giải chi tiết:
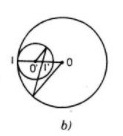
Nếu \((O)\) và \((O’)\) tiếp xúc trong thì tiếp điểm I là tâm vị tự ngoài, tâm vị tự trong I’ xác định như hình vẽ b)
LG c
Một đường tròn chứa đường tròn kia
Lời giải chi tiết:
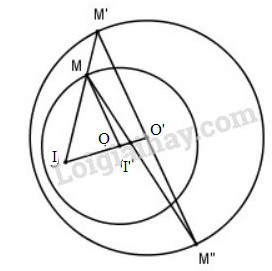
Nếu \((O')\) chứa \((O)\) thì xác định I và I’ như hình vẽ (đặc biệt, khi O trùng O’ thì I và I’ trùng O)

