Cho hình hộp ABCD.A’B’C’D’. Chứng minh rẳng
LG a
mp(BDA’) // mp(B’D’C)
Phương pháp giải:
Mặt phẳng (P) chứa hai đường thẳng cắt nhau cùng song song với (Q) thì (P)//(Q).
Lời giải chi tiết:
Chứng minh ( BDA’) // (B’D’C)
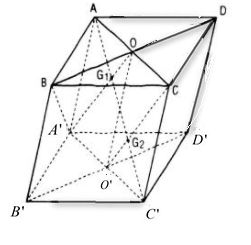
Tứ giác BB’D’D và A’B’CD là các hình bình hành nên : BD // B’D’ và DA’ // B’C
\(BD//B'D' \subset \left( {B'D'C} \right)\)\( \Rightarrow BD//\left( {B'D'C} \right)\)
\(DA'//CB' \subset \left( {B'D'C} \right)\)\( \Rightarrow DA'//\left( {B'D'C} \right)\)
Mà \(BD,DA' \subset \left( {A'BD} \right) \)\(\Rightarrow \left( {A'BD} \right)//\left( {B'D'C} \right)\)
Vậy (BDA’) // (B’D’C).
LG b
Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C
Lời giải chi tiết:

Chứng minh G1 , G2 ∈ AC’
Gọi O, O’ lần lượt là tâm của hình bình hành ABCD và A’B’C’D’.
Trong mặt phẳng (AA’C’C) gọi G1 , G2 lần lượt là giao điểm của AC’ với A’O và O’C.
Ta chứng minh G1, G2 lần lượt là trọng tâm của ∆A’BD và ∆CB’D’.
Thật vậy, ta có ∆G1OA đồng dạng ∆G1A’C’ ( vì AC // A’C’)
\( \Rightarrow {{{G_1}O} \over {{G_1}A'}} = {{OA} \over {A'C'}} = {1 \over 2} \Rightarrow {{A'{G_1}} \over {A'O}} = {2 \over 3}\)
⇒ G1 là trọng tâm ∆A’BD.
Tương tự, G2 là trọng tâm ∆CB’D’. Vậy AC’ đi qua G1, G2 .
LG c
G1 và G2 chia đoạn AC’ thành ba phần bằng nhau
Lời giải chi tiết:
Chứng minh AG1 = G1G2 = G2C’
Theo câu trên , ta có:
\({{A{G_1}} \over {{G_1}C'}} = {{AO} \over {A'C'}} = {1 \over 2}\) ( vì ∆G1OA đồng dạng ∆G1A’C’) \( \Rightarrow A{G_1} = {1 \over 3}AC'\) (1)
Tương tự: \({{C'{G_2}} \over {{G_2}A}} = {{C'O'} \over {CA}} = {1 \over 2}\) ( vì ∆G2C’O' đồng dạng ∆G2AC) \( \Rightarrow C'{G_2} = {1 \over 3}AC'\) (2)
Từ (1) và (2) suy ra: AG1 = G1G2 = G2C’.
LG d
Các trung điểm của sáu cạnh BC, CD, DD’, D’A’, A’B’,B’B cùng nằm trên một mặt phẳng
Lời giải chi tiết:
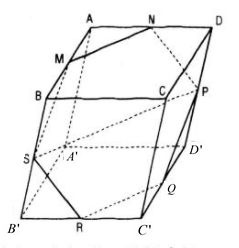
Gọi M, N, P, Q, S, R lần lượt là trung điểm của các cạnh AB, AD, DD’, C’D’, C’B’, B’B.
Ta có: \(\left\{ {\matrix{ {MN//BD} \cr {SP//BD} \cr } } \right. \Rightarrow MN//SP\)
Gọi (α) = (MN, SP)
Ta có : \(\left\{ {\matrix{ {PQ//DC'} \cr {MS//AB'} \cr } } \right. \Rightarrow PQ//MS\)
( vì DC’ // AB’)
⇒ PQ ⊂ (α) do đó Q ∈ (α).
Tương tự: QR // MN ⇒ QR ⊂ (α) do đó R ∈ (α).
Vậy M, N, P, Q, R, S ∈ (α).
Mặt khác vì \(\left\{ {\matrix{ {MS//AB'} \cr {NP//AD'} \cr } } \right.\) nên (MNPQRS) // (AB’D').

