Cho hình tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = 60^\circ ,\widehat {BAD} = 60^\circ .\)
Chứng minh rằng :
LG a
AB ⊥ CD;
Lời giải chi tiết:
Ta có:
\(\eqalign{ & \overrightarrow {AB} .\overrightarrow {CD} \cr &= \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) \cr &= \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \cr & = AB.AD.\cos \widehat {BAD} - AB.AC.\cos \widehat {BAC} = 0 \cr & \Rightarrow AB \bot CD. \cr} \)
(Vì AD=AC và \(\widehat {BAD}=\widehat {BAC}=60^0\).
LG b
Nếu I và J lần lượt là trung điểm của AB và CD thì \(IJ \bot AB\) và \(IJ \bot CD.\)
Lời giải chi tiết:
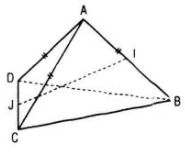
Ta có:
\(\eqalign{ & \overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AJ} \cr & = {1 \over 2}\overrightarrow {BA} + {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {AC} } \right) \cr & = {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right) \cr & = {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} } \right) \cr} \)
Suy ra :
\(\eqalign{ & \overrightarrow {AB} .\overrightarrow {IJ} = {1 \over 2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} - A{B^2}} \right) \cr & ={1 \over 2} \left( {AB.AD.\cos 60^\circ } + AB.AC.\cos 60^\circ - A{B^2} \right) \cr&= 0 \cr & \Rightarrow AB \bot IJ \cr} \)
Mặt khác :
\(\eqalign{ & \overrightarrow {CD} .\overrightarrow {IJ} = {1 \over 2}\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right).\left( {\overrightarrow {AD} + \overrightarrow {BA} + \overrightarrow {AC} } \right) \cr & = {1 \over 2}\left( { - \overrightarrow {AC} .\overrightarrow {AD} + {{\overrightarrow {AD} }^2} + \overrightarrow {CA} .\overrightarrow {BA} + \overrightarrow {AD} .\overrightarrow {BA} - {{\overrightarrow {AC} }^2} + \overrightarrow {AD} .\overrightarrow {AC} } \right) \cr & = - {1 \over 2}\overrightarrow {AB} .\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right) = - {1 \over 2}\overrightarrow {AB} .\overrightarrow {CD} = 0 \cr & \Rightarrow CD \bot IJ \cr} \)

