Đề bài
Đặt một điện áp \({u_L} = 150\sqrt 2 cos100\pi t\)vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần \(60\Omega ,\) cuộn dây (có điện trở thuần) và tụ điện. Công suất tiêu thụ điện của đoạn mạch bằng \(250{\rm{W}}.\) Nối hai bản tụ điện bằng một dây dẫn có điện trở không đáng kể. Khi đó, điện áp hiệu dụng giữa hai đầu điện trở bằng điện áp hiệu dụng giữa hai đầu cuộn dây và bằng \(50\sqrt 3 V.\) Hỏi dung kháng của tụ điện có giá trị bằng bao nhiêu?
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính công suất: \(P = {I^2}(R + r)\)
Sử dụng định luật Ôm \(I = \dfrac{U}{Z}\)
Lời giải chi tiết
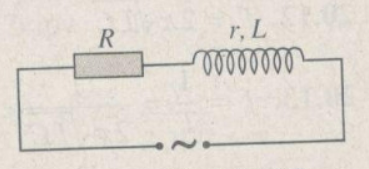
Khi nối tắt tụ điện, mạch còn điện trở \(R\) và cuộn dây
\({U_R} = {U_{Lr}} \Leftrightarrow R = 60 = \sqrt {Z_L^2 + {r^2}} (1)\)
\(\begin{array}{l}{U_R} = IR = \dfrac{{{\rm{UR}}}}{{\sqrt {{{(R + r)}^2} + Z_L^2} }}\\ \Leftrightarrow 50\sqrt 3 = \dfrac{{150.60}}{{\sqrt {{{(60 + r)}^2} + Z_L^2} }}(2)\end{array}\)
Từ (1)(2) giải được \(r = 30\Omega ;{Z_L} = 30\sqrt 3 \Omega \)
Khi tụ không bị nối tắt:
\(\begin{array}{l}P = {I^2}(R + r) = \dfrac{{{U^2}(R + r)}}{{{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}}}\\ \Rightarrow 250 = \dfrac{{{{150}^2}(60 + 30)}}{{{{(60 + 30)}^2} + {{(30\sqrt 3 - {Z_C})}^2}}}\\ \Rightarrow {Z_C} = 30\sqrt 3 \Omega \end{array}\)

