20.5
Đồ thị nào trong Hình \(20.2\) biểu diễn sự biến thiên cường độ dòng điện trong một mạch dao động lí tưởng theo thời gian, nếu lấy mốc thời gian là lúc tụ điện bắt đầu phóng điện trong mạch?
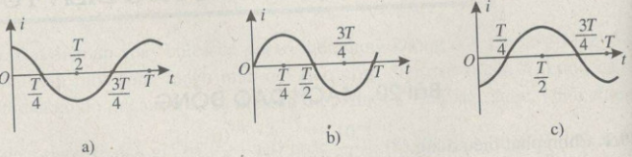
A. Đồ thị a. B. Đồ thị b.
C. Đồ thị c. D. Không có đồ thị nào.
Phương pháp giải:
Sử dụng biểu thức điện tích \(q = {Q_0}{\rm{cos}}\omega {\rm{t}}\) và cường độ dòng điện \(i = {I_{_0}}{\rm{cos(}}\omega t{\rm{ + }}\dfrac{\pi }{2}{\rm{)}}\)
Lời giải chi tiết:
Ta có \(q = {Q_0}{\rm{cos}}\omega {\rm{t}}\); \(i = {I_{_0}}{\rm{cos(}}\omega t{\rm{ + }}\dfrac{\pi }{2}{\rm{)}}\)
Khi tụ bắt đầu phóng điện \(q = {Q_0} \Rightarrow \omega t = 0 \\\Rightarrow i = {I_0}\cos (0 + \dfrac{\pi }{2}) = 0\)
Chọn B
20.6
Sự biến thiên theo thời gian của điện tích \(q\) của một bản tụ điện và của cường độ dòng điện \(i\) trong một mạch dao động lí tưởng được biểu diễn bằng các đồ thị \(q(t)\) (nét liền) và \(i(t)\) (nét đứt) trên cùng một hệ trục tọa độ \(\left[ {(q,i),t} \right]\) ở Hình \(20.3.\) Đồ thị nào đúng? Lấy mốc thời gian là lúc tụ điện bắt đầu phóng điện trong mạch.
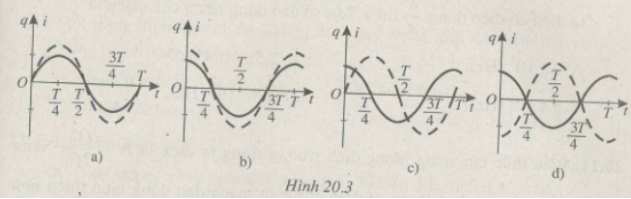
A. Đồ thị a. B. Đồ thị b.
C. Đồ thị c. D. Không có đồ thị nào.
Phương pháp giải:
Sử dụng biểu thức điện tích\(q = {Q_0}{\rm{cos}}\omega {\rm{t}}\) và cường độ dòng điện \(i = {I_{_0}}{\rm{cos(}}\omega t{\rm{ + }}\dfrac{\pi }{2}{\rm{)}}\)
Lời giải chi tiết:
Ta có \(q = {Q_0}{\rm{cos}}\omega {\rm{t}}\); \(i = {I_{_0}}{\rm{cos(}}\omega t{\rm{ + }}\dfrac{\pi }{2}{\rm{)}}\)
Chỉ có đồ thị c) thỏa mãn
Chọn C
20.7
Tần số dao động riêng \(f\) của một mạch dao động lí tưởng phụ thuộc như thế nào vào điện dung \(C\) của tụ điện và độ tự cảm \(L\) của cuộn cảm trong mạch?
A. \(f\) tỉ lệ thuận với \(\sqrt L \) và \(\sqrt C \).
B. \(f\) tỉ lệ nghịch với \(\sqrt L \) và \(\sqrt C \).
C. \(f\) tỉ lệ thuận với \(\sqrt L \) và tỉ lệ nghịch \(\sqrt C \).
D. \(f\) tỉ lệ nghịch với \(\sqrt L \) và tỉ lệ thuận \(\sqrt C \).
Phương pháp giải:
Sử dụng công thức tính tần số \(f = \dfrac{1}{{2\pi \sqrt {LC} }}\)
Lời giải chi tiết:
Ta có tần số \(f = \dfrac{1}{{2\pi \sqrt {LC} }}\)
Suy ra \(f\) tỉ lệ nghịch với \(\sqrt L \) và \(\sqrt C \).
Chọn B

