Đề bài
Một lăng kính có góc chiết quang \(A = {6^0}\) (coi như là góc nhỏ) được đặt trong không khí. Chiếu một chùm ánh sáng trắng song song, hẹp vào mặt bên của lăng kính theo phương vuông góc với mặt phẳng phân giác của góc chiết quang, rất gần cạnh của lăng kính. Đặt một màn ảnh \(E\) sau lăng kính, vuông góc với phương của chùm tia tới và cách mặt phẳng phân giác của góc chiết quang \(1,2m.\) Chiết suất của lăng kính đối với ánh sáng đỏ là \({n_d} = 1,642\) và đối với ánh sáng tím là \({n_t} = 1,685.\) Tính độ rộng từ màu đỏ đến màu tím của quang phổ liên tục quan sát được trên màn ảnh.
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Khi\(A < < \Rightarrow D \approx (n - 1)A\)
Lời giải chi tiết
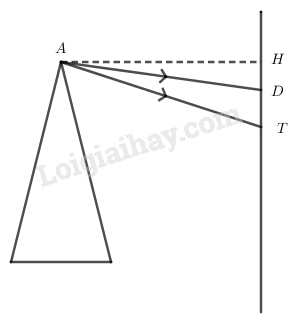
Ta có: Khi \(A < < \Rightarrow D \approx (n - 1)A\)
\( \Rightarrow \left\{ \begin{array}{l}{D_d} = ({n_d} - 1)A\\{D_t} = ({n_t} - 1)A\end{array} \right.\)
Khoảng cách giữa vết sáng đỏ và vết sáng tím thu được trên màn:
\(\begin{array}{l}TD = HT - HD \\= AH.\tan {D_t} - AH.\tan {D_d}\\= f(\tan {D_t} - \tan {D_d}) \\= f({n_t} - {n_d})A \\= 1,2.(1,685 - 1,642).6 = 5,{4.10^{ - 3}}m\\ = 5,4mm\end{array}\)

