Đề bài
Một con lắc đơn gồm một quả cầu nhỏ có khối lượng \(50g\) được treo vào đầu một sợi dây dài \(2m\). Lấy \(g = 9,8m/{s^2}\).
a) Tính chu kì dao động của con lắc khi biên độ góc nhỏ.
b) Kéo con lắc ra khỏi vị trí cân bằng đến vị trí có li độ góc \(\alpha = {30^0}\) rồi buông ra không vận tốc đầu. Tính tốc độ của quả cầu và lực căng \(\overrightarrow F \) của dây khi con lắc đi qua vị trí cân bằng.
Phương pháp giải - Xem chi tiết
a) Sử dụng công thức tính chu kì con lắc: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
b) Sử dụng công thức tính vận tốc và biểu thức định luật II Niuton tính lực căng dây \(F\)
Lời giải chi tiết
Kéo con lắc ra khỏi vị trí cân bằng đến vị trí có li độ góc \(\alpha = {30^0}\) rồi buông ra không vận tốc đầu
\( \Rightarrow \) Biên độ góc \({\alpha _0} = {30^0}\)
a) Chu kì con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} = 2\pi \sqrt {\dfrac{2}{{9,8}}} = 2,8s\)
b) Ta có công thức tính động năng
\(\begin{array}{l}\left\{ \begin{array}{l}{{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\\{{\rm{W}}_d} = mgl(\cos \alpha - \cos {\alpha _0})\end{array} \right.\\ \Rightarrow v = \sqrt {2gl(\cos \alpha - \cos {\alpha _0})} \\ = \sqrt {2.9,8.2(\cos {0^0} - \cos {{30}^0})} \\ = 2,3(m/s)\end{array}\)
Áp dụng định luật II Niuton:
\(\overrightarrow F + \overrightarrow P = m\overrightarrow a \)
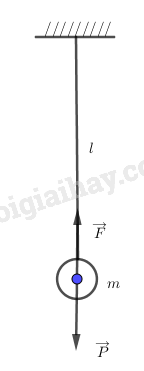
Chiếu theo phương hướng tâm:
\(\begin{array}{l}F - P = m{a_{ht}} = m\dfrac{{{v^2}}}{l}\\ \Leftrightarrow F = P + m\dfrac{{{v^2}}}{l}\\ = P + 2mg(1 - \cos {\alpha _0})\\ = mg + 2mg(1 - \cos {\alpha _0})\\ = mg(3 - 2\cos {\alpha _0})\\ = 0,05.9,8.(3 - 2\cos {30^0}) = 0,62(N)\end{array}\)

