5.5
Hai dao động điều hòa cùng phương, cùng chu kì có phương trình lần lượt là \({x_1} = 4c{\rm{os(4}}\pi {\rm{t + }}\dfrac{\pi }{2})(cm)\) và \({x_2} = 3c{\rm{os(4}}\pi {\rm{t + }}\pi )(cm)\). Biên độ và pha ban đầu của dao động tổng hợp là
A. \(5cm;36,{9^0}\)
B. \(5cm;0,7\pi \left( {ra{\rm{d}}} \right)\)
C. \(5cm;0,2\pi \left( {ra{\rm{d}}} \right)\)
D. \(5cm;0,3\pi \left( {ra{\rm{d}}} \right)\)
Phương pháp giải:
Vận dụng công thức tổng hợp dao động điều hòa: \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi\)
Lời giải chi tiết:
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi = {4^2} + {3^2} + 2.4.3.\cos (\pi - \dfrac{\pi }{2}) = 25\\ \Rightarrow A = 5cm\end{array}\)
Ta có giản đồ Fre-nen:
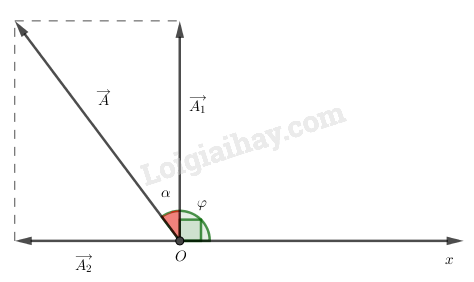
Từ hình vẽ ta thấy: \(\tan \alpha = \dfrac{{{A_2}}}{{{A_1}}} = \dfrac{3}{4} \Rightarrow \alpha = 0,2\pi \Rightarrow \varphi = \alpha + \dfrac{\pi }{2} = 0,7\pi (rad)\)
Chọn B
5.6
Hai dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là \({x_1} = 5c{\rm{os(}}\dfrac{\pi }{2}{\rm{t + }}\dfrac{\pi }{4})(cm)\); \({x_2} = 5c{\rm{os(}}\dfrac{\pi }{2}{\rm{t + }}\dfrac{{3\pi }}{4})(cm)\). Biên độ và pha ban đầu của dao động tổng hợp là
A.\(5cm;\dfrac{\pi }{2}(ra{\rm{d}})\)
B. \(7,1cm;0(ra{\rm{d}})\)
C. \(7,1cm;\dfrac{\pi }{2}(ra{\rm{d}})\)
D. \(7,1cm;\dfrac{\pi }{4}(ra{\rm{d}})\)
Phương pháp giải:
Vận dụng công thức tổng hợp dao động điều hòa: \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi\)
Lời giải chi tiết:
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi = {5^2} + {5^2} + 2.5.5.\cos (\dfrac{{3\pi }}{4} - \dfrac{\pi }{4}) = 50\\ \Rightarrow A = 5\sqrt 2 cm\end{array}\)
Ta có giản đồ Fre-nen:
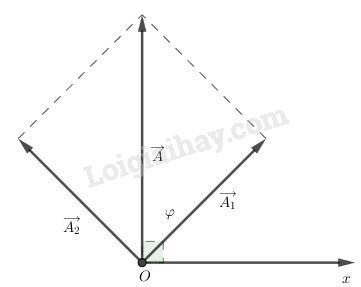
\(\varphi = \dfrac{\pi }{2}rad\)
Chọn C

