Đề bài
Một con lắc đơn dài \(1,2m\) dao động tại một nơi có gia tốc rơi tự do \(g = 9,8m/{s^2}\). Kéo con lắc ra khỏi vị trí cân bằng theo chiều dương một góc \({\alpha _0} = {10^0}\) rồi thả tay.
a) Tính chu kì dao động của con lắc
b) Viết phương trình dao động của con lắc.
c) Tính tốc độ và gia tốc của quả cầu con lắc khi nó đi qua vị trí cân bằng.
Phương pháp giải - Xem chi tiết
a) Sử dụng công thức tính chu kì con lắc:\(T = 2\pi \sqrt {\dfrac{l}{g}} \)
b) Vận dụng các bước viết phương trình dao động điều hòa: tìm \(\omega \), tìm \({\alpha _0}\), tìm pha ban đầu\(\varphi \)
c) Sử dụng công thức tính vận tốc và gia tốc.
Lời giải chi tiết
a) Chu kì con lắc: \(T = 2\pi \sqrt {\dfrac{l}{g}} = 2\pi \sqrt {\dfrac{{1,2}}{{9,8}}} = 2,2(s)\)
b) Viết phương trình dao động:
+Tần số góc \(\omega = \sqrt {\dfrac{g}{l}} = \sqrt {\dfrac{{9,8}}{{1,2}}} = 2,86(rad/s)\)
+ Biên độ \({\alpha _0} = {10^0} = \dfrac{\pi }{{18}}rad \Rightarrow A = {\alpha _0}.l = \dfrac{\pi }{{18}}.1,2 = 0,21m\)
+ Pha ban đầu \(\varphi \)
\(t = 0:{x_0} = A\cos \varphi = A \Rightarrow \varphi = 0\)
Vậy phương trình dao động điều hòa:\(x = 0,21\cos (2,86t)(m)\)
c) Tại vị trí cân bằng:
+ Tốc độ: \(v = A.\omega = 0,21.2,86 = 0,6m/s\)
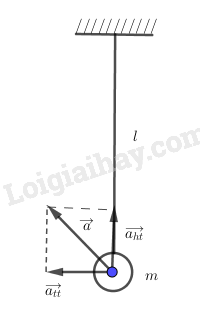
+ Gia tốc: \(a = \sqrt {a_{tt}^2 + a{}_{ht}^2} \)
Mà:
\(\begin{array}{l}\left\{ \begin{array}{l}{a_{tt}} = 0\\{a_{ht}} = 2g(\cos \alpha - \cos {\alpha _0}) = 2.9,8(\cos {0^0} - \cos {10^0}) = 0,3(m/{s^2})\end{array} \right.\\ \Rightarrow a = 0,3(m/{s^2})\end{array}\)
Chú ý:
Gia tốc con lắc đơn tổng hợp 2 vecto gia tốc thành phần: gia tốc theo phương tiếp tuyến \(\overrightarrow {{a_{tt}}} \) và gia tốc theo phương hướng tâm \(\overrightarrow {{a_{ht}}}\)