8.3
Hai nguồn phát sóng đồng bộ \({S_1},{S_2}\) nằm sâu trong một bể nước. \(M\) và \(N\) là điểm trong bể nước có hiệu khoảng cách tới \({S_1}\)và \({S_2}\) bằng một số bán nguyên lần bước sóng. \(M\) nằm trên đường thẳng \({S_1}{S_2}\); \(N\) nằm ngoài đường thẳng đó (\(H.8.1\) ).
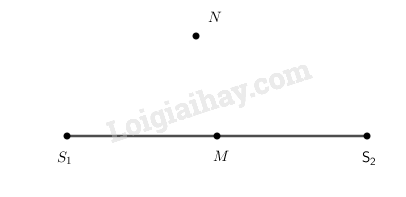
Chọn phát biểu đúng:
A. Các phần tử nước ở \(M\) và \(N\) đều đứng yên.
B. Các phần tử nước ở \(M\) và \(N\) đều dao động.
C. Các phần tử nước ở \(M\) dao động, ở \(N\) đứng yên.
D. Các phần tử nước ở \(M\) đứng yên, ở \(N\) dao động.
Phương pháp giải:
Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha: \({d_2} - {d_1} = k\lambda \); cực tiểu: \({d_2} - {d_1} = (k + \dfrac{1}{2})\lambda \)
Lời giải chi tiết:
\(M\) và \(N\) là điểm trong bể nước có hiệu khoảng cách tới \({S_1}\) và \({S_2}\) bằng một số bán nguyên lần bước sóng, thỏa mãn điều kiện cực tiểu
\( \Rightarrow \) Các phần tử nước tại \(M\) và \(N\) đều đứng yên
Chọn A
8.4
Ở mặt nước có hai nguồn kết hợp \(A,B\) dao động theo phương thẳng đứng với phương trình \({u_A} = {u_B} = 2cos20\pi t(mm)\). Tốc độ truyền sóng là \(30cm/s\). Coi biên độ sóng không đổi khi sóng truyền đi. Phần tử \(M\) ở mặt nước cách hai nguồn lần lượt là \(10,5cm\) và \(13,5cm\) có biên độ dao động là
A. \(1mm\) B. \(0mm\)
C. \(2mm\) D. \(4mm\)
Phương pháp giải:
Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha: \({d_2} - {d_1} = k\lambda \); cực tiểu: \({d_2} - {d_1} = (k + \dfrac{1}{2})\lambda \)
Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}{d_{2M}} = 13,5cm\\{d_{1M}} = 10,5cm\end{array} \right.\)
Tần số \(f = \dfrac{\omega }{{2\pi }} = \dfrac{{20\pi }}{{2\pi }} = 10Hz\)
Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{30}}{{10}} = 3cm\)
Ta có \({d_{2M}} - {d_{1M}} = 13,5 - 10,5 \\= 3cm = 1.\lambda \)
\( \Rightarrow \) tại M là một cực đại \( \Rightarrow {A_M} = 2a = 2.2 = 4cm\)

