Đề bài
Cho hai dao động điều hòa cùng phương, cùng tần số góc là \(2\pi \left( {ra{\rm{d}}/s} \right)\) , có biên độ lần lượt \(2cm\) và \(4cm\), có pha ban đầu lần lượt là \(\dfrac{\pi }{6}\) và \(\dfrac{\pi }{2}(ra{\rm{d}})\).
a) Viết phương trình của hai dao động.
b) Biểu diễn trên cùng một giản đồ Fre-nen hai vectơ quay biểu diễn hai dao động trên.
c) Tìm phương trình dao động tổng hợp của hai dao động trên.
Phương pháp giải - Xem chi tiết
a) Sử dụng lí thuyết về phương trình dao động điều hòa
b) Vận dụng lí thuyết về giản đồ Fre-nen
c) Vận dụng công thức tổng hợp dao động điều hòa
Lời giải chi tiết
a) Phương trình dao động điều hòa của hai dao động là:
\(\begin{array}{l}{x_1} = 2\cos (2\pi t + \dfrac{\pi }{6})(cm)\\{x_2} = 4\cos (2\pi t + \dfrac{\pi }{2})(cm)\end{array}\)
b) Hai vecto quay trên giản đồ Fre-nen
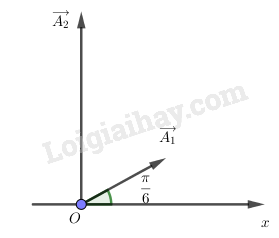
c)
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi\\ = {2^2} + {4^2} + 2.2.4.\cos (\dfrac{\pi }{2} - \dfrac{\pi }{6}) = 28\\ \Rightarrow A = 2\sqrt 7 cm\end{array}\)
Ta có giản đồ Fre-nen:
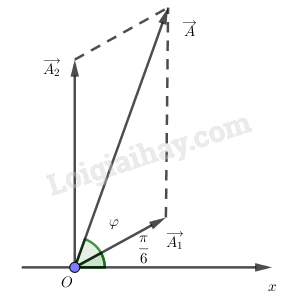
Ta có:
\(\begin{array}{l}\tan \varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2}}}\\ = \dfrac{{2\sin \dfrac{\pi }{6} + 4\sin \dfrac{\pi }{2}}}{{2\cos \dfrac{\pi }{6} + 4\cos \dfrac{\pi }{2}}} = \dfrac{{5\sqrt 3 }}{3}\\ \Rightarrow \varphi = 1,2(rad)\end{array}\)
Phương trình dao động tổng hợp là: \(x = 2\sqrt 7 \cos (2\pi t + 1,2)(cm)\)

