Đề bài
Một vật dao động điều hoà dọc theo trục \({\rm{Ox}}\), quanh điểm gốc \(O\), với biên độ \(A = 24cm\) và chu kì \(T = 4s\). Tại thời điểm \(t = 0\), vật có li độ là \( - A\).
a) Viết phương trình dao động của vật.
b) Tính li độ, vận tốc và gia tốc của vật tại thời điểm \(t = 0,5s\).
c) Xác định thời điểm đầu tiên vật qua vị trí có li độ \(x = - 12cm\) và tốc độ tại thời điểm đó.
Phương pháp giải - Xem chi tiết
a) Sử dụng các bước viết phương trình dao động điều hòa: tìm \(\omega \), tìm \(A\), tìm pha ban đầu \(\varphi \)
b) Thay t vào biểu thức li độ, vận tốc, gia tốc
c) Sử dụng vòng tròn lượng giác tính thời gian
Sử dụng công thức tính tốc độ \(v = \omega \sqrt {{A^2} - {x^2}} \)
Lời giải chi tiết
a) Viết phương trình dao động của vật
+ Tần số góc: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{4} = \dfrac{\pi }{2}(rad/s)\)
+ Biên độ: \(A = 24cm\)
+ Tìm \(\varphi \): \(t = 0:{x_0} = A\cos \varphi = - A \Leftrightarrow \cos \varphi = - 1 \Leftrightarrow \varphi = \pi (rad)\)
Vậy phương trình dao động: \(x = 24\cos (\dfrac{\pi }{2}t + \pi )(cm)\)
b)Phương trình vận tốc: \(v = - {\rm{A}}\omega {\rm{sin(}}\omega {\rm{t + }}\varphi ) = - 24.\dfrac{\pi }{2}.\sin (\dfrac{\pi }{2}t + \pi )(cm/s)\)
Phương trình gia tốc: \(a = - A{\omega ^2}\cos (\omega t + \varphi ) = - 12.{(\dfrac{\pi }{2})^2}\cos (\dfrac{\pi }{2}t + \pi )(cm/{s^2})\)
Tại thời điểm \(t = 0,5s\):
Li độ: \(x = 24\cos (\dfrac{\pi }{2}t + \pi ) = 24\cos (\dfrac{\pi }{2}.0,5 + \pi ) = - 12\sqrt 2 (cm)\)
Vận tốc: \(v = - 24.\dfrac{\pi }{2}.\sin (\dfrac{\pi }{2}t + \pi ) = - 24.\dfrac{\pi }{2}.\sin (\dfrac{\pi }{2}.0,5 + \pi ) = 26,7(cm/s)\)
Gia tốc: \(a = - 12.{(\dfrac{\pi }{2})^2}\cos (\dfrac{\pi }{2}t + \pi ) = - 12.{(\dfrac{\pi }{2})^2}\cos (\dfrac{\pi }{2}.0,5 + \pi ) = 41,9(cm/{s^2})\)
c) Thời điểm đầu tiên vật đi qua li độ \(x = - 12cm\) là
Vị trí xuất phát: \(x = - A\)
Vị trí đích: \(x = - 12cm = - \dfrac{A}{2}cm\)
Vẽ vòng tròn lượng giác:
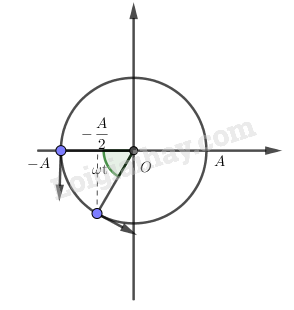
Từ hình vẽ: \(\cos (\omega t) = \dfrac{1}{2} \Rightarrow \omega t = \dfrac{\pi }{3} \Leftrightarrow \dfrac{\pi }{2}t = \dfrac{\pi }{3} \Leftrightarrow t = \dfrac{2}{3}s\)
Tốc độ tại thời điểm đó: \(v = \omega \sqrt {{A^2} - {x^2}} = \dfrac{\pi }{2}\sqrt {{{24}^2} - {{( - 12)}^2}} = 32,6(cm/s)\)

