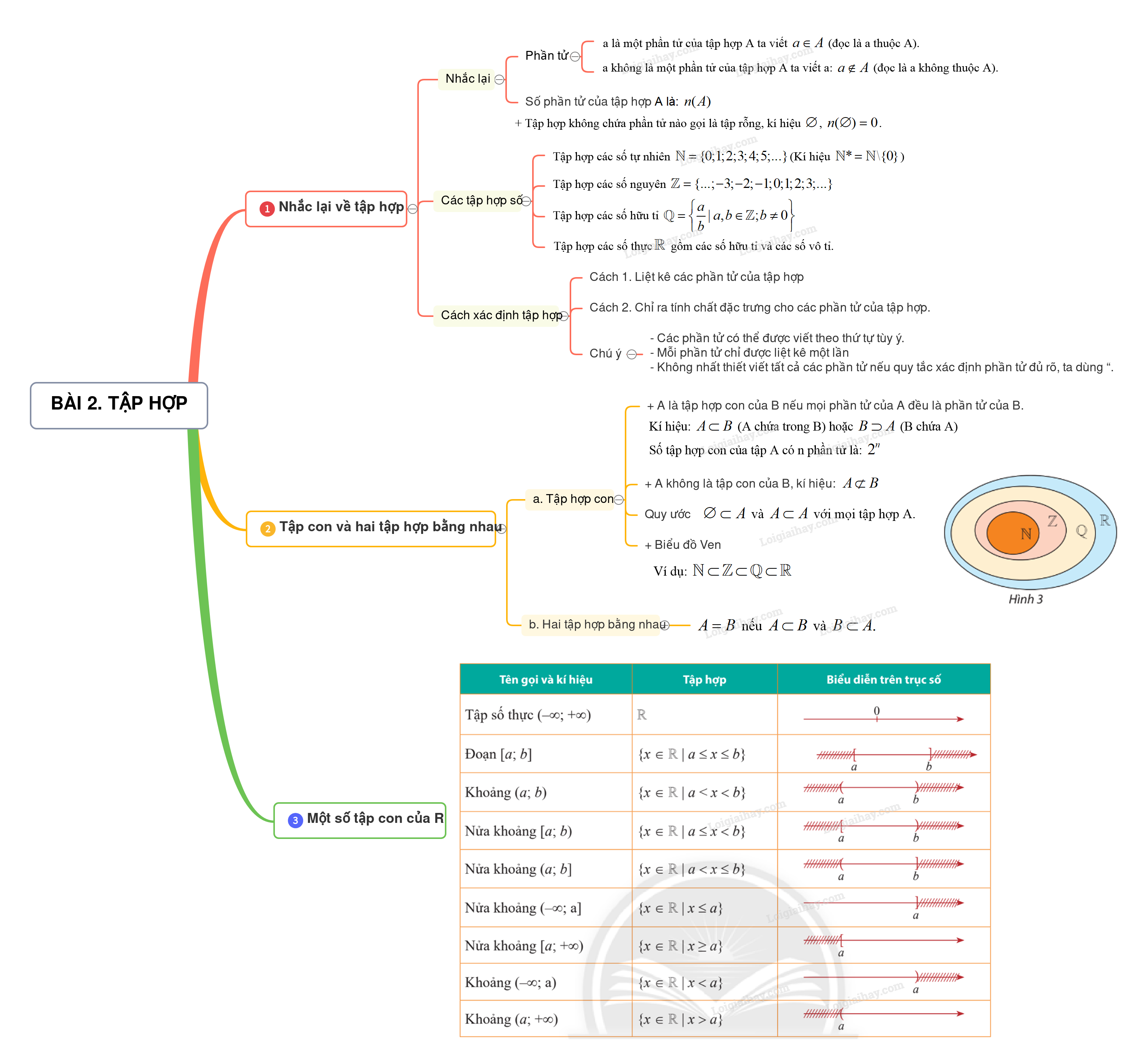
1. Nhắc lại về tập hợp
+ a là một phần tử của tập hợp A ta viết \(a \in A\) (đọc là a thuộc A).
a không là một phần tử của tập hợp A ta viết a: \(a \notin A\) (đọc là a không thuộc A).
+ Số phần tử của tập hợp A kì hiệu là \(n(A)\)
+ Tập hợp không chứa phần tử nào gọi là tập rỗng, kí hiệu \(\emptyset \), \(n(\emptyset ) = 0\).
+ Các tập hợp số
Tập hợp các số tự nhiên \(\mathbb{N} = \{ 0;1;2;3;4;5;...\} \)(Kí hiệu \(\mathbb{N}* = \mathbb{N}{\rm{\backslash }}\{ 0\} \))
Tập hợp các số nguyên \(\mathbb{Z} = \{ ...; - 3; - 2; - 1;0;1;2;3;...\} \)
Tập hợp các số hữu tỉ \(\mathbb{Q} = \left\{ {\frac{a}{b}|a,b \in \mathbb{Z};b \ne 0} \right\}\)
(Gồm các số nguyên và các số thập phân hữu hạn hoặc vô hạn tuần hoàn)
Tập hợp các số thực\(\mathbb{R}\) gồm các số hữu tỉ và các số vô tỉ.
(Số vô tỉ là các số thập phân vô hạn không tuần hoàn).
+ Cách xác định tập hợp:
Cách 1. Liệt kê các phần tử của tập hợp;
Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
* Lưu ý:
- Các phần tử có thể được viết theo thứ tự tùy ý.
- Mỗi phần tử chỉ được liệt kê một lần
- Không nhất thiết viết tất cả các phần tử nếu quy tắc xác định phần tử đủ rõ, ta dùng “…”
2. Tập con và hai tập hợp bằng nhau
a. Tập hợp con
- Cho hai tập hợp A và B.
+ A là tập hợp con của B nếu mọi phần tử của A đều là phần tử của B.
Kí hiệu: \(A \subset B\) (A chứa trong B) hoặc \(B \supset A\) (B chứa A)
Số tập hợp con của tập A có n phần tử là: \({2^n}\)
+ A không là tập con của B, kí hiệu: \(A \not\subset B\)
- Quy ước: \(\emptyset \subset A\) và \(A \subset A\) với mọi tập hợp A.
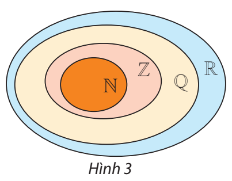
+ Biểu đồ Ven
Ví dụ: \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
b. Hai tập hợp bằng nhau
\(A = B\) nếu \(A \subset B\) và \(B \subset A.\)
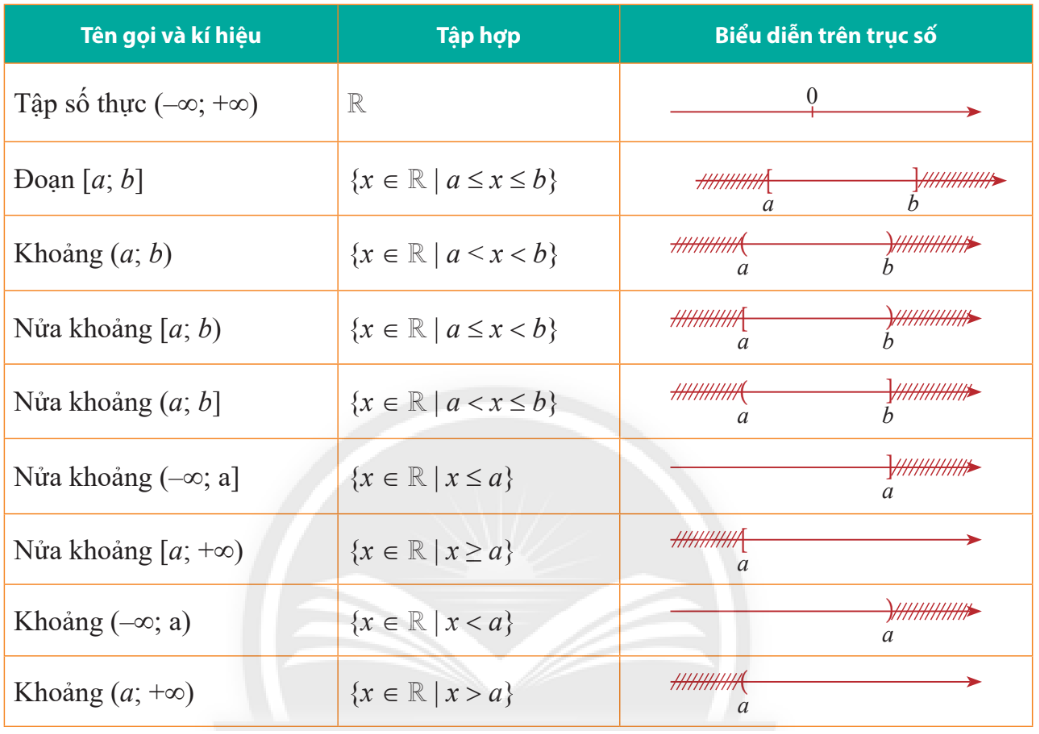
3. Một số tập con của \(\mathbb{R}\)