Đề bài
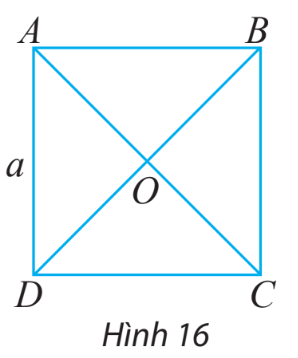
Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\)
Phương pháp giải - Xem chi tiết
a) Bước 1: Tìm độ dài các cạnh \(AB,BC,CD,DA,AC,BD...\)
Bước 2: Xác định hướng của các vectơ có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
Bước 3: Từ bước 2, chỉ ra hai vectơ cùng hướng
Lời giải chi tiết
a) \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).
Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là:
\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).
