HĐ Khởi động
Lời giải chi tiết:
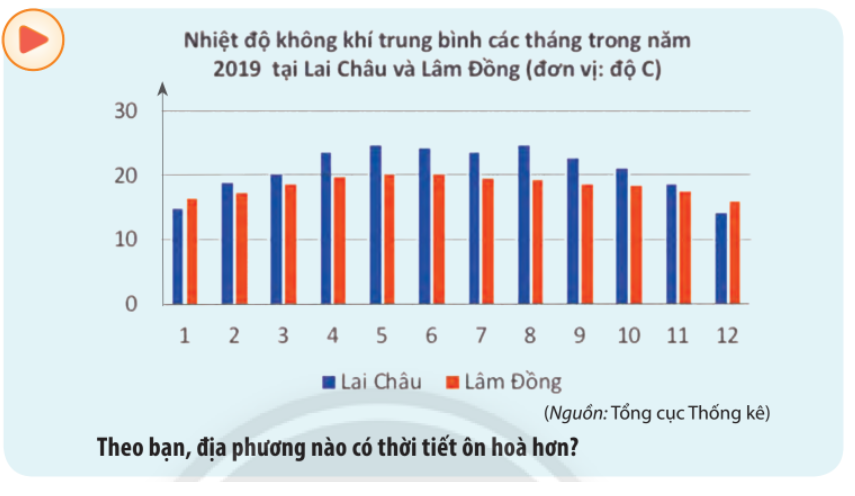
Nếu so sánh nhiệt độ trung bình thì 2 địa phương đều có thời tiết ôn hòa dễ chịu. Tuy nhiên so sánh sự chên lệch nhiệt độ giữa các tháng thì Lâm Đồng có thời tiết ôn hòa hơn do tháng thấp nhất là khoảng 15 độ (cao hơn Lai Châu) và sự chênh lệch nhiệt độ giữa các tháng không lớn (khoảng 4 độ C).
HĐ Khám phá 1
Thời gian hoàn thành bài chạy 5 km (tính theo phút) của hai nhóm thanh niên được cho ở bảng sau:
| Nhóm 1 | 30 | 32 | 47 | 31 | 32 | 30 | 32 | 29 | 17 | 29 | 32 | 31 |
| Nhóm 2 | 32 | 29 | 32 | 30 | 32 | 31 | 29 | 31 | 32 | 30 | 31 | 29 |
a) Hãy tính độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong từng nhóm.
b) Nhóm nào có thành tích chạy đồng đều hơn?
Phương pháp giải:
a) Độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 1 là:
47−17=30 (phút)
Độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 2 là:
32−29=3(phút)
b) Dễ thấy: nhóm 2 có thành tích chạy đồng đều hơn.
Thực hành 1
Hãy tìm khoảng biến thiên và khoảng tứ phân vị của các mẫu số liệu sau:
a) 10;13;15;2;10;19;2;5;7
b) 15;19;10;5;9;10;1;2;5;15
Phương pháp giải:
Cho mẫu số liệu: x1,x2,...,xn
Sắp xếp mẫu số liệu theo thứ tự không giảm: X1,X2,...,Xn
+) Khoảng biến thiên: R=Xn−X1
+) Tứ phân vị: Q1,Q2,Q3
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: X1,X2,...,Xn
Bước 2: Q2=Me={Xk+1(n=2k+1)12(Xk+Xk+1)(n=2k)
Q1 là trung vị của nửa số liệu đã sắp xếp bên trái Q2 (không bao gồm Q2 nếu n lẻ)
Q3 là trung vị của nửa số liệu đã sắp xếp bên phải Q2 (không bao gồm Q2 nếu n lẻ)
Khoảng tứ phân vị: ΔQ=Q3−Q1
Lời giải chi tiết:
a) Xét mẫu số liệu đã sắp xếp là: 2;2;5;7;10;10;13;15;19
Khoảng biến thiên của mẫu số liệu là: R=19−2=17.
Cỡ mẫu là n=9 là số lẻ nên giá trị tứ phân vị thứ hai là: Q2=10.
Tứ phân vị thứ nhất là trung vị của mẫu: 2;2;5;7. Do đó Q1=3,5
Tứ phân vị thứ ba là trung vị của mẫu: 10;13;15;19. Do đó Q3=14
Khoảng tứ phân vị của mẫu là: ΔQ=14−3,5=10,5
b) Xét mẫu số liệu đã sắp xếp là: 1;2;5;5;9;10;10;15;15;19
Khoảng biến thiên của mẫu số liệu là: R=19−1=18.
Cỡ mẫu là n=10 là số chẵn nên giá trị tứ phân vị thứ hai là: Q2=9,5.
Tứ phân vị thứ nhất là trung vị của mẫu: 1;2;5;5;9. Do đó Q1=5.
Tứ phân vị thứ ba là trung vị của mẫu: 10;10;15;15;19. Do đó Q3=15
Khoảng tứ phân vị của mẫu là: ΔQ=15−5=10
Vận dụng 1
Dưới đây lfa bảng số liệu thống kê của Biểu đồ nhiệt trung bình các tháng trong 2019 của hai tình Lai Châu và Lâm Đồng (được đề cập đến ở hoạt động khởi động của bài học)
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Lai Châu | 14,8 | 18,8 | 20,3 | 23,5 | 24,7 | 24,2 | 23,6 | 24,6 | 22,7 | 21,0 | 18,6 | 14,2 |
| Lâm Đồng | 16,3 | 17,4 | 18,7 | 19,8 | 20,2 | 20,3 | 19,5 | 19,3 | 18,6 | 18,5 | 17,5 | 16,0 |
a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm đồng.
b) Hãy cho biết trong một năm, nhiệt độ ở địa phương nào ít thay đổi hơn.
Phương pháp giải:
a) Cho mẫu số liệu: x1,x2,...,xn
Sắp xếp mẫu số liệu theo thứ tự không giảm: X1,X2,...,Xn
+) Khoảng biến thiên: R=Xn−X1
+) Tứ phân vị: Q1,Q2,Q3
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: X1,X2,...,Xn
Bước 2: Q2=Me={Xk+1(n=2k+1)12(Xk+Xk+1)(n=2k)
Q1 là trung vị của nửa số liệu đã sắp xếp bên trái Q2 (không bao gồm Q2 nếu n lẻ)
Q3 là trung vị của nửa số liệu đã sắp xếp bên phải Q2 (không bao gồm Q2 nếu n lẻ)
Khoảng tứ phân vị: ΔQ=Q3−Q1
b) So sánh khoảng biến thiên
Lời giải chi tiết:
a)
+) Tỉnh Lai Châu: Xét mẫu số liệu đã sắp xếp là:
14,214,818,618,820,321,022,723,523,624,224,624,7
Khoảng biến thiên của mẫu số liệu là: R=24,7−14,2=10,5.
Cỡ mẫu là n=12 là số chẵn nên giá trị tứ phân vị thứ hai là: Q2=21,85.
Tứ phân vị thứ nhất là trung vị của mẫu: 14,214,818,618,820,321,0. Do đó Q1=18,7.
Tứ phân vị thứ ba là trung vị của mẫu: 22,723,523,624,224,624,7. Do đó Q3=23,9
Khoảng tứ phân vị của mẫu là: ΔQ=23,9−18,7=5,2
+) Tỉnh Lâm Đổng: Xét mẫu số liệu đã sắp xếp là:
16,016,317,417,518,518,618,719,319,519,820,220,3
Khoảng biến thiên của mẫu số liệu là: R=20,3−16,0=4,3.
Cỡ mẫu là n=12 là số chẵn nên giá trị tứ phân vị thứ hai là: Q2=18,65.
Tứ phân vị thứ nhất là trung vị của mẫu: 16,016,317,417,518,518,6. Do đó Q1=17,45.
Tứ phân vị thứ ba là trung vị của mẫu: 18,719,319,519,820,220,3. Do đó Q3=19,65
Khoảng tứ phân vị của mẫu là: ΔQ=19,65−17,45=2,2
Thực hành 2
Hãy tìm giá trị ngoại lệ của mẫu số liệu: 37; 12; 3; 9; 10; 9; 12; 3; 10.
Phương pháp giải:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: X1,X2,...,Xn
Bước 2: Q2=Me={Xk+1(n=2k+1)12(Xk+Xk+1)(n=2k)
Q1 là trung vị của nửa số liệu đã sắp xếp bên trái Q2 (không bao gồm Q2 nếu n lẻ)
Q3 là trung vị của nửa số liệu đã sắp xếp bên phải Q2 (không bao gồm Q2 nếu n lẻ)
Khoảng tứ phân vị: ΔQ=Q3−Q1
Bước 3: Tìm x trong mẫu sao cho x>Q3+1,5ΔQ hoặc x<Q1−1,5ΔQ
Lời giải chi tiết:
Xét mẫu số liệu đã sắp xếp là:
3;3;9;9;10;10;12;12;37.
Cỡ mẫu là n=9 là số lẻ nên giá trị tứ phân vị thứ hai là: Q2=10.
Tứ phân vị thứ nhất là trung vị của mẫu: 3;3;9;9.. Do đó Q1=6.
Tứ phân vị thứ ba là trung vị của mẫu: 10;12;12;37.. Do đó Q3=12
Khoảng tứ phân vị của mẫu là: ΔQ=12−6=6
Giá trị ngoại lệ x thỏa mãn x>12+1,5.6=21 hoặc x<6−1,5.6=−3.
Vậy giá trị ngoại lệ của mẫu số liệu đó là 37

