Đề bài
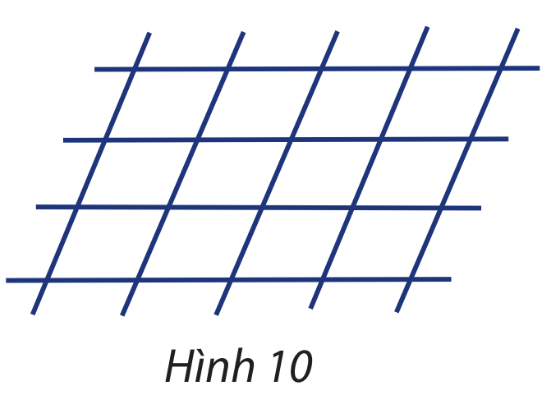
Có 4 đường thẳng song song cắt 5 đường thẳng song song khác tạo thành những hình bình hành (như hình 10). Có bao nhiêu hình bình hành được tạo thành?
Phương pháp giải - Xem chi tiết
Bước 1: Chọn 2 đường thẳng song song trong 4 đường
Bước 2: Chọn 2 đường thẳng song song từ 5 đường kia
Bước 3: Áp dụng quy tắc nhân
Lời giải chi tiết
Ta thấy rằng, cứ 2 đường thẳng song song cắt 2 đường thẳng song song khác thì tạo thành một hình bình hành
Do đó, hình bình hành tạo thành được xác định qua 2 công đoạn
Công đoạn 1: Chọn 2 đường thẳng song song với nhau trong 4 đường thẳng, mỗi cách chọn 2 đường thẳng từ 4 đường là một tổ hợp chập 2 của 4. Do đó, số cách chọn 2 đường thẳng từ 4 đường thẳng là:
\(C_4^2 = \frac{{4!}}{{2!.2!}} = 6\)
Công đoạn 2: Chọn 2 đường thẳng song song với nhau trong 5 đường thẳng bị cắt bởi 2 đường kia, mỗi cách chọn 2 đường thẳng từ 5 đường là một tổ hợp chập 2 của 5. Do đó, số cách chọn 2 đường thẳng từ 5 đường thẳng là: \(C_4^2 = \frac{{5!}}{{2!.3!}} = 10\)
Áp dụng quy tắc nhân, ta có số hình bình hành được tạo thành là:
\(6.10 = 60\) (hình bình hành)

