Đề bài
Cho hình bình hành ABCD
a) Chứng minh \(2\left( {A{B^2} + B{C^2}} \right) = A{C^2} + B{D^2}\)
b) Cho \(AB = 4,BC = 5,BD = 7.\) Tính AC.
Phương pháp giải - Xem chi tiết
a)
Bước 1. Tính góc AC, BD theo AB, BC, cosA dựa vào định lí cosin
Bước 2: Biến đối để suy ra đẳng thức
b) Theo câu a: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\), từ đó suy ra AC.
Lời giải chi tiết
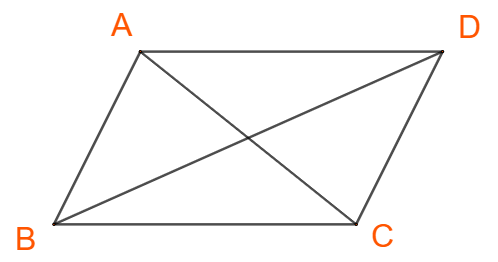
a) Áp dụng định lí cosin ta có:
\(\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\end{array} \right.\)
Mà \(AD = BC;\cos A = \cos ({180^ \circ } - B) = - \cos B\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos A\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos A\end{array} \right.\\ \Rightarrow A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\end{array}\)
b) Theo câu a, ta suy ra: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\)
\(\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}\)
