Đề bài
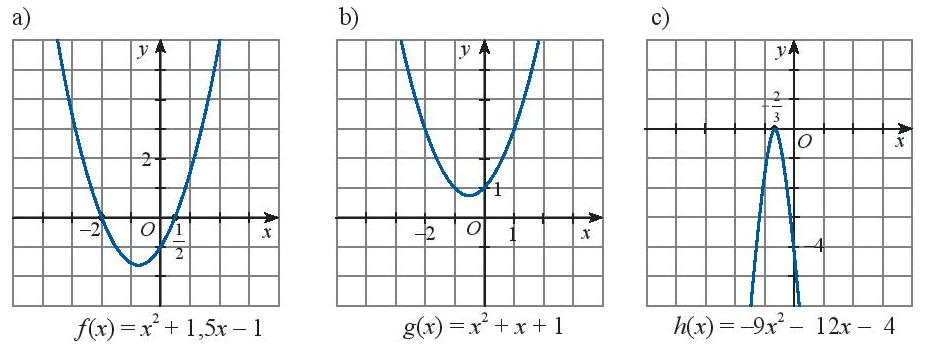
Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng

Phương pháp giải - Xem chi tiết
Bước 1: Xác định nghiệm của tam thức (là giao điểm của đồ thị với trục hoành)
Bước 2: Xác định khoảng mà \(f\left( x \right) > 0\) (khoảng đồ thị nằm trên trục hoành)
Bước 3: Xác định khoảng mà \(f\left( x \right) < 0\) (khoảng đồ thị nằm dưới trục hoành)
Bước 4: Lập bảng xét dấu
Lời giải chi tiết
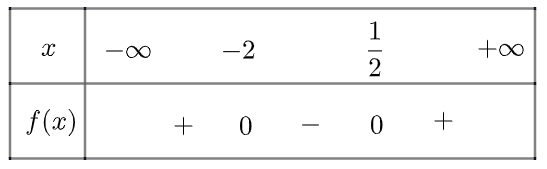
a) Tam thức \(f\left( x \right) = {x^2} + 1,5x - 1\) có hai nghiệm phân biệt \({x_1} = - 2;{x_2} = \frac{1}{2}\)
\(\)\(f\left( x \right) > 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{1}{2}, + \infty } \right)\) và \(f\left( x \right) < 0\) khi \(x \in \left( { - 2,\frac{1}{2}} \right)\)
Ta có bảng xét dấu như sau
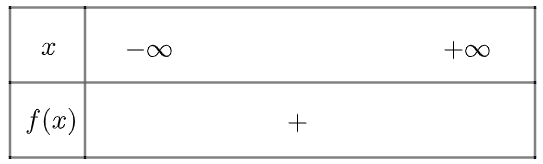
b) Tam thức \(g\left( x \right) = {x^2} + x + 1\) vô nghiệm, \(g\left( x \right) > 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau
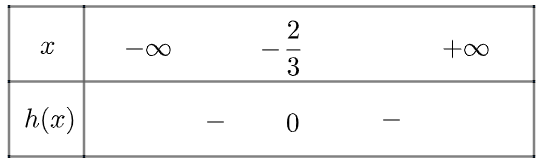
c) Tam thức \(h\left( x \right) = - 9{x^2} - 12x - 4\) có nghiệm kép \({x_1} = {x_2} = - \frac{2}{3}\) và \(h\left( x \right) < 0\forall x \ne - \frac{2}{3}\)
Ta có bảng xét dấu như sau
d) Tam thức \(f\left( x \right) = - 0,5{x^2} + 3x - 6\) vô nghiệm và \(f\left( x \right) < 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau:

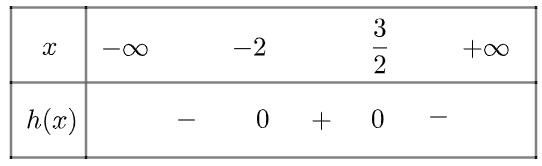
e) Tam thức \(g\left( x \right) = - {x^2} - 0,5x + 3\) có hai nghiệm \({x_1} = - 2,{x_2} = \frac{3}{2}\)
\(g\left( x \right) > 0\) khi \(x \in \left( { - 2,\frac{3}{2}} \right)\) và \(g\left( x \right) < 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{3}{2}, + \infty } \right)\)
Ta có bảng xét dấu như
g) Tam thức \(h\left( x \right) = {x^2} + 2\sqrt 2 x + 2\) có nghiệm kép \({x_1} = {x_2} = - \sqrt 2 \)
\(h\left( x \right) > 0\forall x \ne - \sqrt 2 \)
Ta có bảng xét dấu như sau


