HĐ Khám phá 4
a) Cho điểm M là trung điểm của đoạn thẳng AB. Ta đã biết →MB=−→MA=→AM.−−→MB=−−−→MA=−−→AM. Hoàn thành phép cộng vectơ sau: →MA+→MB=→MA+→AM=→MM=?−−→MA+−−→MB=−−→MA+−−→AM=−−−→MM=?
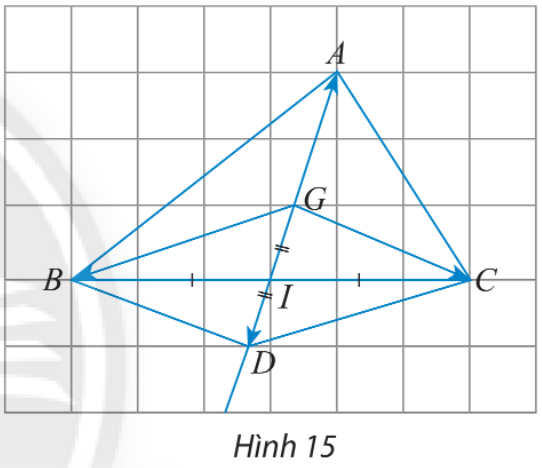
b) Cho điểm G là trọng tâm của tam giác ABC có trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Ta có BGCD là hình bình hành và G là trung điểm của đoạn thẳng AD. Với lưu ý rằng →GB+→GC=→GD−−→GB+−−→GC=−−→GD và →GA=→DG−−→GA=−−→DG, hoàn thành các phép cộng vectơ sau:
→GA+→GB+→GC=→GA+→GD=→DD=?−−→GA+−−→GB+−−→GC=−−→GA+−−→GD=−−→DD=?
Phương pháp giải:
a) Thay thế các vectơ bằng nhau →MB=−→MA=→AM.−−→MB=−−−→MA=−−→AM.
b) Bước 1: Áp dụng quy tắc hình bình hành trên BGCD
Bước 2: Áp dụng tính chất trung điểm vừa tìm được ở câu a) →MA+→MB=→0−−→MA+−−→MB=→0
(với M là trung điểm của AB)
Lời giải chi tiết:
a) →MA+→MB=→MA+→AM=→MM=→0−−→MA+−−→MB=−−→MA+−−→AM=−−−→MM=→0 (vì vectơ →MB=−→MA=→AM.−−→MB=−−−→MA=−−→AM.)
b) Xét hình bình hành BGCD ta có: →GB+→GC=→GD−−→GB+−−→GC=−−→GD
⇒→GA+→GB+→GC=→GA+→GD=→DG+→GD=→DD=→0⇒−−→GA+−−→GB+−−→GC=−−→GA+−−→GD=−−→DG+−−→GD=−−→DD=→0
(vì →GA=−→GD=→DG−−→GA=−−−→GD=−−→DG)
Thực hành 5
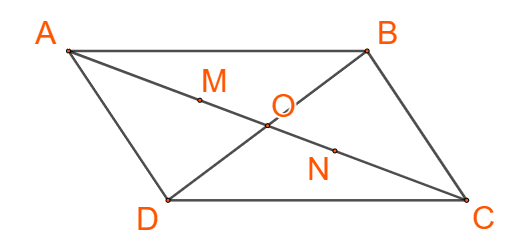
Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:
a) →MA+→MD+→MB=→0−−→MA+−−→MD+−−→MB=→0
b) →ND+→NB+→NC=→0
c) →PM+→PN=→0
Phương pháp
a) Sử dụng tính chất trọng tâm của tam giác →GA+→GB+→GC=→0(với G là trọng tâm của tam giác ABC)
b) Sử dụng tính chất trọng tâm của tam giác →GA+→GB+→GC=→0
c) Sử dụng tính chất trung điểm →MA+→MB=→0(với M là trung điểm của AB)
Phương pháp giải:
a) Sử dụng tính chất trọng tâm của tam giác →GA+→GB+→GC=→0(với G là trọng tâm của tam giác ABC)
b) Sử dụng tính chất trọng tâm của tam giác →GA+→GB+→GC=→0
c) Sử dụng tính chất trung điểm →MA+→MB=→0(với M là trung điểm của AB)
Lời giải chi tiết:
a) Áp dụng tính chất trọng tâm ta có: →MA+→MD+→MB=→0
Suy ra M là trọng tâm của tam giác ADB
Vậy M nằm trên đoạn thẳng AO sao cho AM=23AO
b) Tiếp tục áp dụng tính chất trọng tâm →ND+→NB+→NC=→0
Suy ra N là trọng tâm của tam giác BCD
Vậy N nằm trên đoạn thẳng OD sao cho ON=13OD
c) Áp dụng tính chất trung điểm ta có: →PM+→PN=→0
Suy ra P là trung điểm của đoạn thẳng MN
Vậy điểm P trùng với điểm O