Đề bài
Một công ty cần mua các tủ đựng hồ sơ. Có hai loại tủ: Tủ loại A chiếm 3 \({m^2}\) sàn, loại này có sức chứa 12 \({m^3}\) và có giá 7,5 triệu đồng; tủ loại B chiếm 6 \({m^2}\) sàn, loại này có sức chứa 18 \({m^3}\) và có giá 5 triệu. Cho biết công ty chỉ thu xếp được nhiều nhất là 60 \({m^2}\) mặt bằng cho chỗ đựng hồ sơ và ngân sách mua tủ không quá 60 triệu đồng. Hãy lập kế hoạch mua sắm để công ty có được thể tích đựng hồ sơ lớn nhất.
Lời giải chi tiết
Gọi x, y lần lượt là số tủ loại A, loại B mà công ty cần mua.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Mặt bằng nhiều nhất là 60 \({m^2}\) nên \(3x + 6y \le 60\)
- Ngân sách mua tủ không quá 60 triệu đồng nên \(7,5x + 5y \le 60\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}3x + 6y \le 60\\7,5x + 5y \le 60\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.
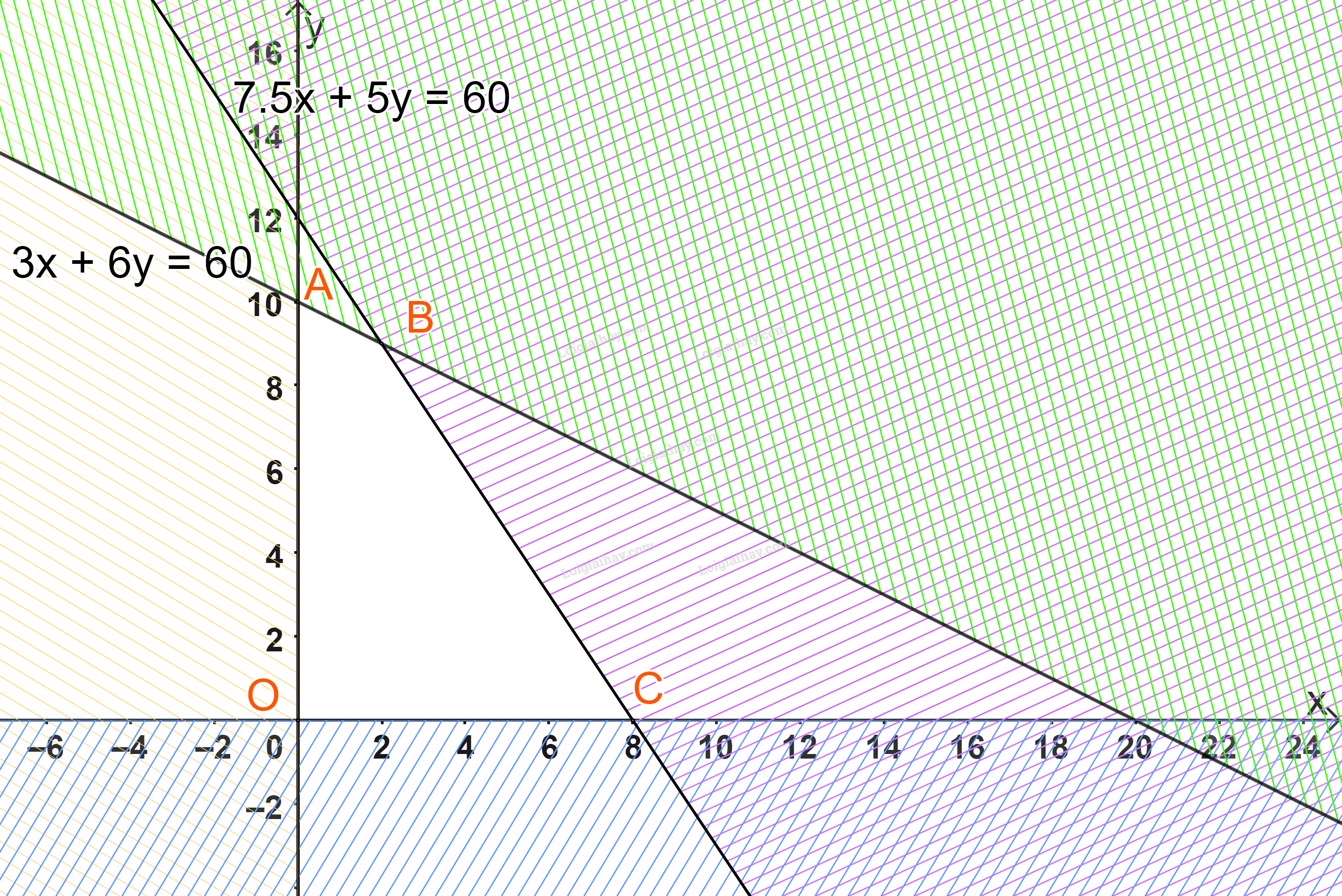
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(0;10),\)\(B(2;9),\)\(C(8;0).\)
Gọi F là số tiền lãi (đơn vị: triệu đồng) thu về, ta có: \(F = 12x + 18y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 12.0 + 18.0 = 0\)
Tại \(A(0;10):\)\(F = 12.0 + 18.10 = 180\)
Tại \(B(2;9),\)\(F = 12.2 + 18.9 = 186\)
Tại \(C(8;0).\)\(F = 12.8 + 18.0 = 96\)
F đạt giá trị lớn nhất bằng \(186\) tại \(B(2;9),\)
Vậy công ty đó nên mua 2 tủ loại A và 9 tủ loại B để thể tích đựng hồ sơ là lớn nhất.
