Đề bài
Lớp 10C có 45 học sinh, trong đó có 18 học sinh tham gia cuộc thi vẽ đồ họa trên máy tính, 24 học sinh tham gia cuộc thi tin học văn phòng cấp trường và 9 học sinh không tham gia cả hai cuộc thi này. Hỏi có bao nhiêu học sinh của lớp 10C tham gia đồng thời hai cuộc thi?
Phương pháp giải - Xem chi tiết
Gọi A là tập hợp các học sinh tham gia cuộc thi vẽ đồ họa trên máy tính và B là tập hợp các học sinh tham gia cuộc thi tin học văn phòng cấp trường.
Vẽ biểu đồ Ven.
Lời giải chi tiết
Gọi X là tập hợp các học sinh của lớp 10C.
A là tập hợp các học sinh tham gia cuộc thi vẽ đồ họa trên máy tính,
B là tập hợp các học sinh tham gia cuộc thi tin học văn phòng cấp trường.
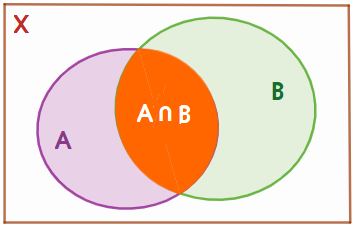
Theo biểu đồ Ven ta có: \(n(A) = 18,\;n(B) = 24,\;n(X) = 45.\)
\(n(A \cup B)\) là số học sinh tham gia ít nhất một trong hai cuộc thi, bằng: 45 -9 = 36 (học sinh)
Mà \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\) (do các học sinh tham gia cả 2 cuộc thi được tính hai lần)
Suy ra số học sinh tham gia cả 2 cuộc thi là: \(n(A \cap B) = 18 + 24 - 36 = 6\)
Vậy có 6 học sinh của lớp 10C tham gia đồng thời hai cuộc thi.

