HĐ Khám phá 1
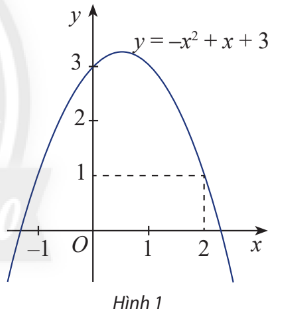
Đồ thị của hàm số y=f(x)=−x2+x+3được biểu diễn trong hình 1
a) Biểu thức f(x) là đa thức bậc mấy?
b) Xác định dấu của f(2)
Phương pháp giải:
a) Xác định số mũ cao nhất
b) Thay x=2 vào f(x), so sánh với 0.
Lời giải chi tiết:
a) Số mũ cao nhất của hàm số là 2, suy ra biểu thứcf(x)đã cho là đa thức bậc hai
b) Thay x=2 vào f(x) ta có:
f(2)=−22+2+3=1>0
Suy ra f(2) dương.
Thực hành 1
Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại x=1.
a) f(x)=2x2+x−1;
b) g(x)=−x4+2x2+1
c) h(x)=−x2+√2.x−3
Lời giải chi tiết:
a) Biểu thức f(x)=2x2+x−1 là một tam thức bậc hai
f(1)=2.12+1−1=2>0 nên f(x) dương tại x=1
b) Biểu thức g(x)=−x4+2x2+1 không phải là một tam thức bậc hai
c) Biểu thức h(x)=−x2+√2.x−3 là một tam thức bậc hai
h(1)=−12+√2.1−3=√2−4<0 nên h(x) âm tại x=1
Thực hành 2
Tìm biệt thức và nghiệm của các tam thức bậc hai sau:
a) f(x)=2x2−5x+2
b) g(x)=−x2+6x−9
c) h(x)=4x2−4x+9
Phương pháp giải:
Bước 1: Xác định biệt thức Δ=b2−4ac
Bước 2: Xét dấu của Δ
Bước 3: Tìm nghiệm
+) Nếu Δ>0⇒x1=−b+√Δ2a;x2=−b−√Δ2a
+) Nếu Δ=0⇒x1=x2=−b2a
+) Nếu Δ=0thì tam thức bậc hai vô nghiệm
Lời giải chi tiết:
a) Tam thức bậc hai f(x)=2x2−5x+2 có Δ=(−5)2−4.2.2=9
Δ>0, do đó f(x) có hai nghiệm phân biệt là
x1=5+√94=2 và x1=5−√94=12
b) Tam thức bậc hai g(x)=−x2+6x−9 có Δ=62−4.(−1).(−9)=0
Δ=0, do đó g(x)có nghiệm kép x1=x2=−62.(−1)=3
c) Tam thức bậc hai h(x)=4x2−4x+9 có Δ=(−4)2−4.4.9=−128
Δ<0, do đó h(x) vô nghiệm

