Đề bài
Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:
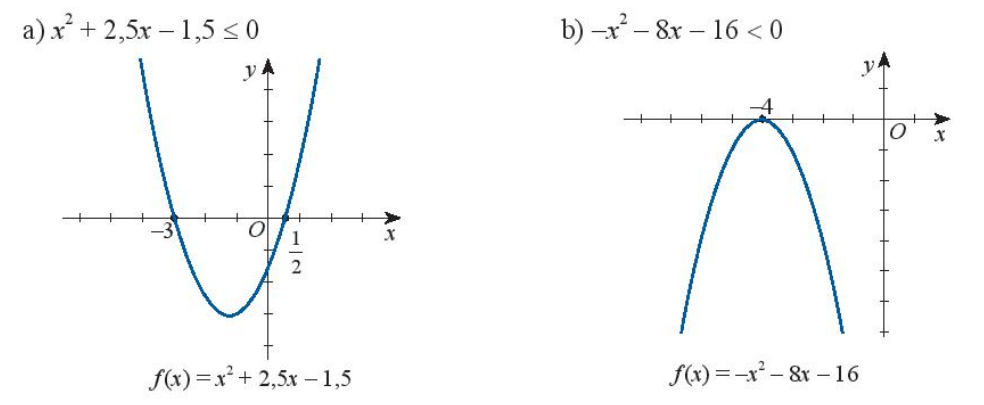
Phương pháp giải - Xem chi tiết
+) Phần đồ thị nằm trên trục hoành có các x tương ứng là nghiệm của BPT f(x)>0
+) Phần đồ thị nằm dưới trục hoành có các x tương ứng là nghiệm của BPT f(x)<0
+) Tại x có đồ thị cắt trục hoành là nghiệm của BPT f(x)=0
Lời giải chi tiết
a) Dựa vào đồ thị ta thấy x2+2,5x−1,5≤0 khi x thuộc đoạn [−3;12]
Vậy nghiệm của bất phương trình x2+2,5x−1,5≤0 là [−3;12]
b) Dựa vào đồ thị ta thấy −x2−8x−16<0 với mọi x khác −4
Vậy nghiệm của bất phương trình −x2−8x−16<0 là R∖{−4}
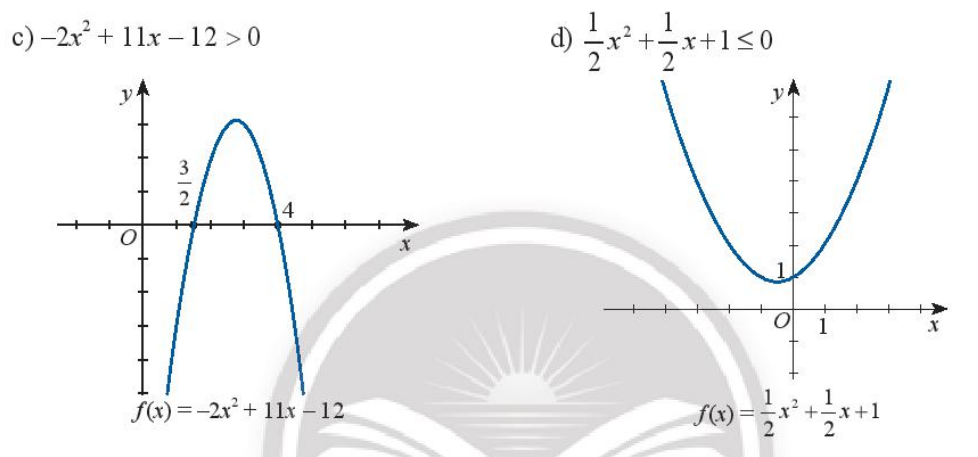
c) Dựa vào đồ thị ta thấy −2x2+11x−12>0 khi x thuộc khoảng (32;4)
Vậy nghiệm của bất phương trình −2x2+11x−12>0 là (32;4)
d) Dựa vào đồ thị ta thấy đồ thị của tam thức f(x)=12x2+12x+1 nằm hoàn toàn phía trên trục hoành với mọi x
Vậy bất phương trình 12x2+12x+1≤0 vô nghiệm.

