Đề bài
Một nông trại thu hoạch được 180 kg cà chua và 15 kg hành tây. Chủ nông trại muốn làm các hũ tương cà để bán. Biết rằng, để làm ra một hũ tương cà loại A cần 10 kg cà chua cùng với l kg hành tây và khi bán lãi được 200 nghìn đồng, còn để làm được một hũ tương cà loại B cần 5 kg cà chua cùng với 0,25 kg hành tây và khi bán lãi được 150 nghìn đồng. Thǎm dò thị hiếu của khách hàng cho thấy cần phải làm số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B. Hãy giúp chủ nông trại lập kế hoạch làm tương cà để có được nhiều tiền lãi nhất.
Lời giải chi tiết
Gọi x, y lần lượt là số hũ tương cà loại A, loại B mà chủ nông trại cần làm.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Có 180 kg cà chua nên \(10x + 5y \le 180\)
- Có 15 kg hành tây nên \(x + 0,25y \le 15\)
- Số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B nên \(x \ge 3,5y\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}10x + 5y \le 180\\x + 0,25y \le 15\\x \ge 3,5y\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.
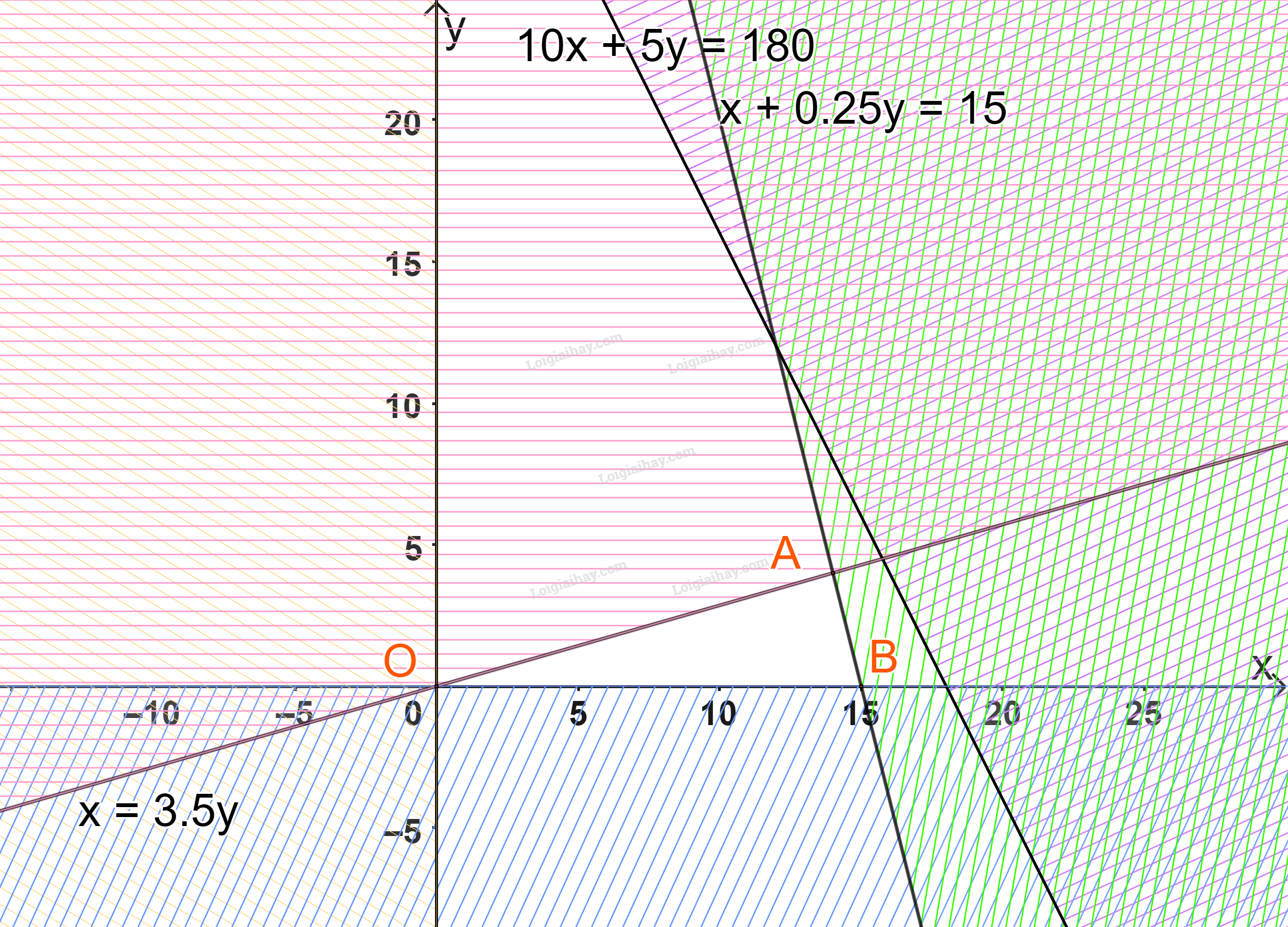
Miền không gạch chéo (miền tam giác OAB, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(14;4),\)\(B(15;0).\)
Gọi F là số tiền lãi (đơn vị: nghìn đồng) thu được, ta có: \(F = 200x + 150y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 200.0 + 150.0 = 0\)
Tại \(A(14;4),\)\(F = 200.14 + 150.4 = 3400\)
Tại \(B(15;0),\)\(F = 200.15 + 150.0 = 3000\)
F đạt giá trị lớn nhất bằng \(3400\) nghìn đồng tại \(A(14;4).\)
Vậy chủ nông trại đó nên làm 14 hũ loại A và 4 hũ loại B để tiền lãi thu được là lớn nhất.

