Đề bài
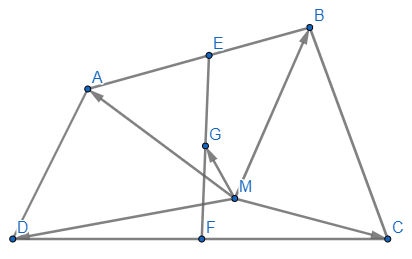
Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng →MA+→MB+→MC+→MD=4→MG
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc ba điểm →MA=→MO+→OA và tính chất trung điểm →OA+→OB=→0
(với O là trung điểm của AB)
Lời giải chi tiết
→MA+→MB+→MC+→MD=(→MG+→GE+→EA)+(→MG+→GE+→EB)+(→MG+→GF+→FC)+(→MG+→GF+→FD)
=(→MG+→MG+→MG→+MG)+2(→GE+→GF)+(→EA+→EB)+(→FC+→FD)
=4→MG+2.→0+→0+→0=4→MG (đpcm)

