Đề bài
Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ Oxy:
{x−2y>0x+3y<3
Phương pháp giải - Xem chi tiết
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên cùng một mặt phẳng Oxy
Lời giải chi tiết
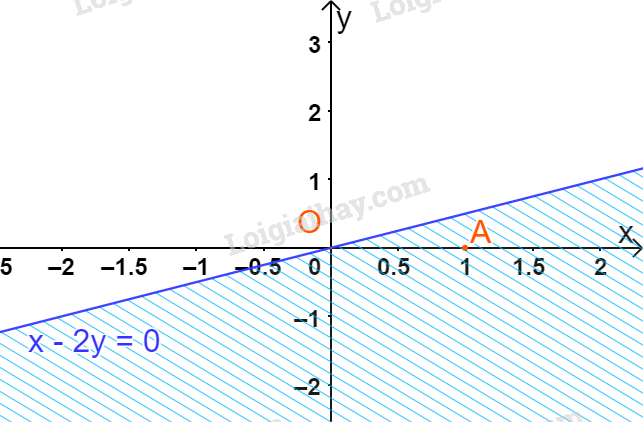
Vẽ đường thẳng d:x−2y=0 đi qua hai điểm O(0;0) và B(2;1)
Xét gốc tọa độ A(0;1). Ta thấy A∉Δ và 0−2.1=−2<0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ d, không chứa điểm A
(miền không gạch chéo trên hình)
Vẽ đường thẳng d′:x+3y=3 đi qua hai điểm A′(0;1) và B′(3;0)
Xét gốc tọa độ O(0;0). Ta thấy O∉Δ và 0+3.0=0<3
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ d′, chứa gốc tọa độ O
(miền không gạch chéo trên hình)
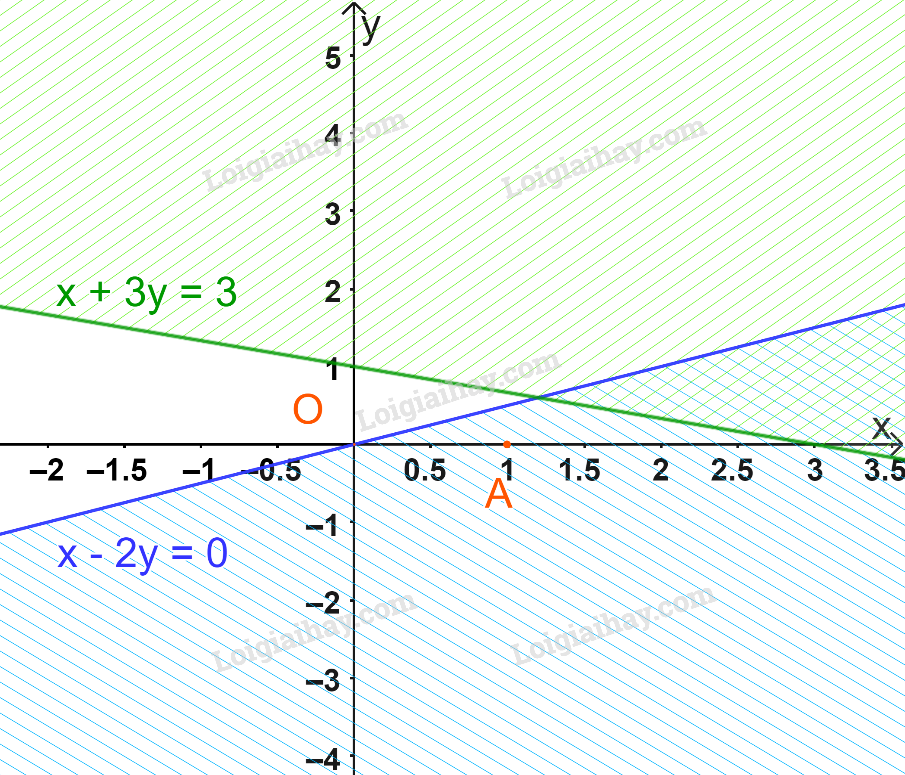
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho.

