HĐ Khám phá 3
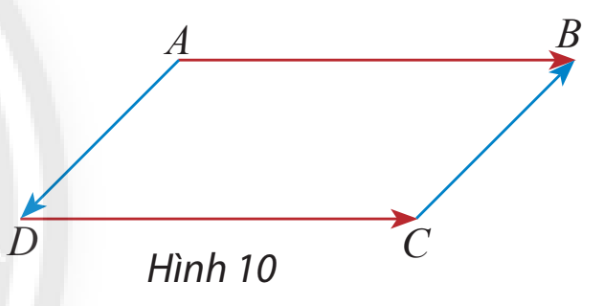
Cho hình bình hành ABCD (hình 30), hãy so sánh độ dài và hướng của hai vectơ :
a) và
b) và
Lời giải chi tiết:
a) Ta có:
và , có hướng từ trái sang phải
Suy ra và cùng hướng
b) Ta có:
và có hướng từ trên xuống dưới, có hướng từ dưới lên trên. Suy ra và ngược hướng
Thực hành 5
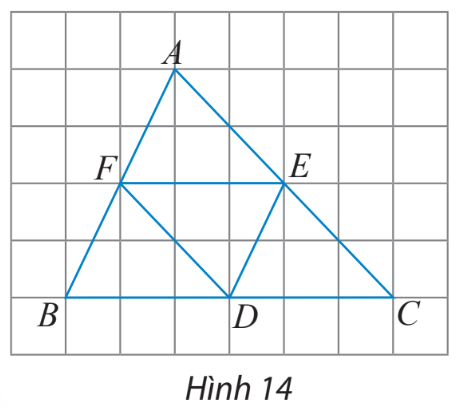
Cho D, E, F lần lượt là trung điểm của cạnh BC, CA, AB của tam giác ABC (hình 14).
a) Tìm các vectơ bằng vectơ .
b) Tìm các vectơ đối vectơ
Phương pháp giải:
a)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ
Bước 2: Trong đó liệt kê các vectơ cùng hướng với vectơ
b)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ
Bước 2: Trong đó liệt kê các vectơ ngược hướng với vectơ
Lời giải chi tiết:
Từ giả thiết ta có:
; ;
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ là và
b) Các vectơ đối vectơ là và