Đề bài
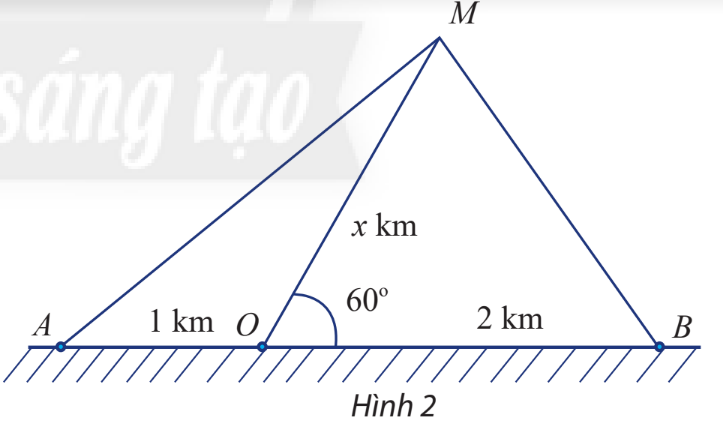
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60∘. Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng 1km và 2km (Hình 2).
a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.
b) Tìm x để khoảng cách từ tàu đến B bằng 45 khoảng cách từ tàu đến A
c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.
Lưu ý: Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải - Xem chi tiết
a) Sử dụng định lý cosin a2=b2+c2+2bccosA
b) Lập phương trình MB=45MA, và giải phương trình lập được
c) Lập phương trình MB=MO−0,5, và giải phương trình lập được
Lời giải chi tiết
a) Đặt độ dài của MO là x km (x>0)
Ta có: ^MOA+^MOB=180∘ (hai góc bù nhau) ⇒^MOA=120∘
Áp dụng định lý Cosin trong tam giác ta tính được:
+) Khoảng cách từ tàu đến B là MB=√x2+22−2.2.x.cos60∘=√x2−2x+4
+) Khoảng cách từ tàu đến A là MA=√x2+12−2.1.x.cos120∘=√x2+x+1
b) Theo giải thiết ta có phương trình MB=45MA⇒√x2−2x+4=45√x2+x+1
⇒x2−2x+4=1625(x2+x+1)⇒925x2−6625x+8425=0
⇒x≃1,64 và x≃5,69
Thay hai nghiệm vừa tìm được vào phương trình √x2−2x+4=45√x2+x+1 ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi x≃1,64 hoặc x≃5,69 thì khoảng cách từ tàu đến B bằng 45 khoảng cách từ tàu đến A
c) Đổi 500 m = 0,5 km
Theo giả thiết ta có phương trình sau:
MB=MO−0,5⇒√x2−2x+4=x−0,5⇒x2−2x+4=(x−0,5)2⇒x2−2x+4=x2−x+14⇒x=154
Thay x=154 vào phương trình √x2−2x+4=x−0,5 ta thấy thỏa mãn phương trình
Vậy khi x=154 thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.

