1. GIÁ TRỊ LƯỢNG GIÁC
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\) có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị để \(\widehat {xOM} = \alpha .\)Khi đó:
\(\sin \alpha = {y_0}\) là tung độ của M
\(\cos \alpha = {x_0}\) là hoành độ của M
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\)
2. QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU
Hai góc bù nhau, \(\alpha \) và \({180^o} - \alpha \):
\(\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha ({0^o} < \alpha < {180^o})\end{array}\)
Hai góc phụ nhau, \(\alpha \) và \({90^o} - \alpha \):
\(\begin{array}{l}\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}\)
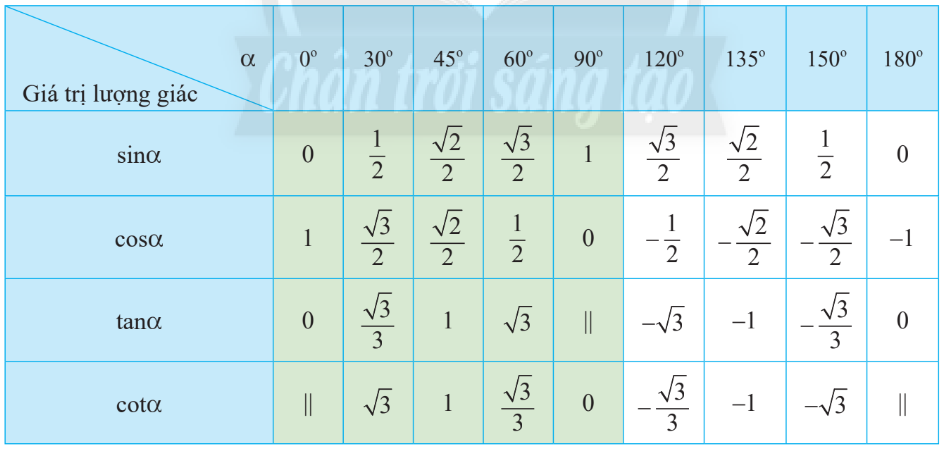
3. CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT SỐ GÓC ĐẶC BIỆT
4. SỬ DỤNG MÁY TÍNH CẦM TAY ĐỂ TÍNH CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC
a) Tính các giá trị lượng giác của góc
Bước 1: Cài đặt đơn vị đo góc (độ hoặc radian)
Bước 2: Vào chế độ tính toán
Chú ý: Để tính \(\cot \alpha \) ta tính \(\frac{1}{{\tan \alpha }}\).
b) Xác định số đo của góc khi biết giá trị lượng giác của góc đó
Để tìm \(\alpha \) khi biết \(\cot \alpha \) ta tính \(\tan \alpha = \frac{1}{{\cot \alpha }}\) rồi tính \(\alpha \) sau.

