HĐ Khám phá 3
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.

Phương pháp giải:
Quan sát đồ thị hàm số trên các khoảng (−∞;−b2a) và (−b2a;+∞)
Trên (a’; b’): đồ thị có dạng đi lên từ trái sang phải thì hàm số đó đồng biến trên (a’;b’).
Trên (c; d): đồ thị có dạng đi xuống từ trái sang phải thì hàm số đó nghịch biến trên (c;d).
Lời giải chi tiết:
a)
Trên (−∞;−b2a) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên (−∞;−b2a)
Trên (−b2a;+∞) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên (−b2a;+∞)
Vậy hàm số có khoảng đồng biến là (−b2a;+∞), khoảng nghịch biến là (−∞;−b2a)
b)
Trên (−∞;−b2a) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên (−∞;−b2a)
Trên (−b2a;+∞) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên (−b2a;+∞)
Vậy hàm số có khoảng đồng biến là (−∞;−b2a), khoảng nghịch biến là (−b2a;+∞)
Thực hành 3
Tìm khoảng đồng biến, khoảng nghịch biến của hàm số y=2x2−6x+11. Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?
Phương pháp giải:
Lập bảng biến thiên, xác định khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số.
Lời giải chi tiết:
Đỉnh S có tọa độ: xS=−b2a=−(−6)2.2=32;yS=2.(32)2−6.32+11=132.
Hay S(32;132).
Vì hàm số bậc hai có a=2>0 nên ta có bảng biến thiên sau:
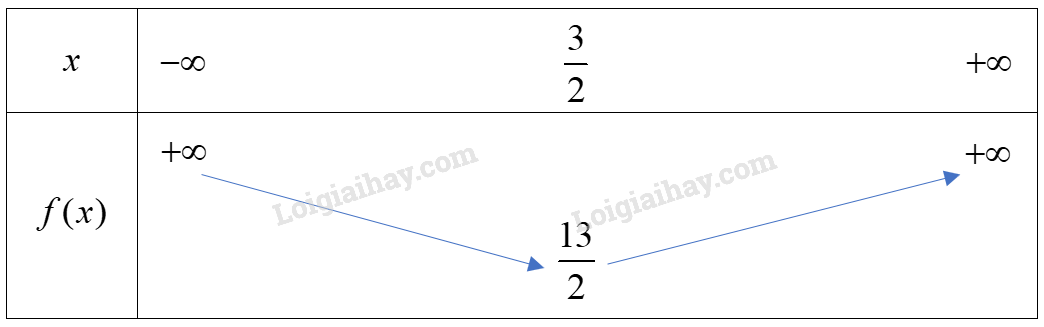
Hàm số đồng biến trên khoảng (32;+∞) và nghịch biến trên khoảng (−∞;32)
Hàm số đạt giá trị nhỏ nhất bằng 132 khi x=32
Do đó hàm số không thể đạt giá trị bằng -1 vì −1<132.

