Giải bài 5 trang 65 SGK Toán 10 tập 1 – Chân trời sáng tạo

163 lượt xem

Bài trước

Bài sau

Lựa chọn câu để xem lời giải nhanh hơn

Chứng minh rằng với mọi góc $\alpha \;\;({0^o} \le \alpha \le {180^o})$ , ta đều có:

LG a

a) ${\cos ^2}\alpha + {\sin ^2}\alpha = 1$

Phương pháp giải:

Lấy điểm M trên nửa đường tròn đơn vị sao cho $\alpha = \widehat {xOM}$

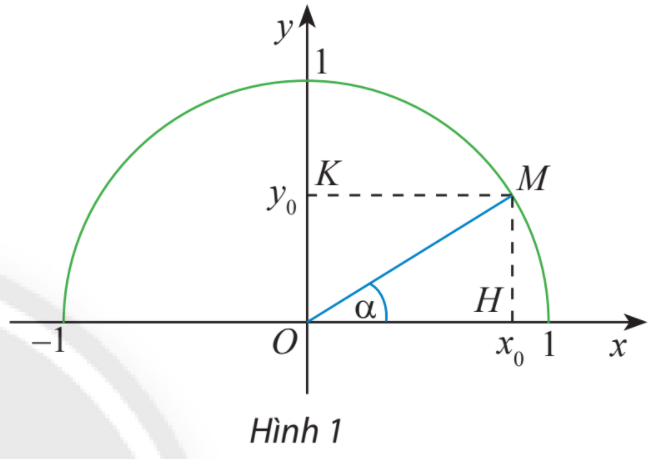
$\sin \alpha = \frac{{MH}}{{OM}};\;\cos \alpha = \frac{{OH}}{{OM}};\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.$

Lời giải chi tiết:

Trên nửa đường tròn đơn vị, lấy điểm M sao cho $\widehat {xOM} = \alpha$

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

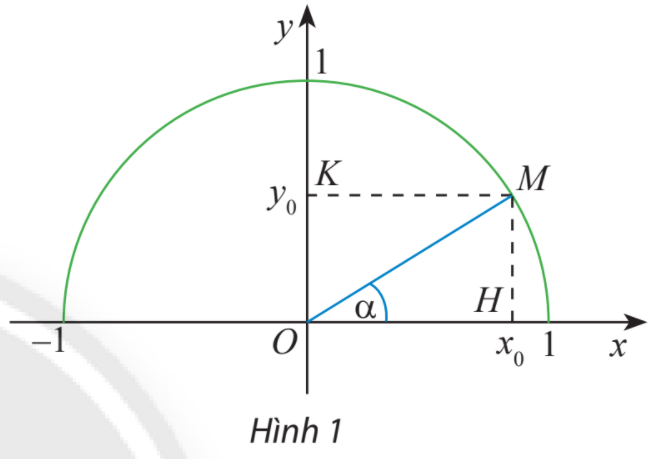
Ta có: tam giác vuông OHM vuông tại H và $\alpha = \widehat {xOM}$

Do đó: $\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.$

$\Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1$

LG b

b) $\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})$

Lời giải chi tiết:

Ta có:

$\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}$

LG c

c) $1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})$

Lời giải chi tiết:

Với $\alpha \ne {90^o}$ ta có:

$\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}$

LG d

d) $1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})$

Lời giải chi tiết:

Ta có:

$\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}$

Xem thêm các chương trình khác:

Bài trước

Bài sau

SGK Toán - Chân trời sáng tạo