Đề bài
Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng
a) →AC+→BD=2→MN
b) →AC+→BD=→BC+→AD
Phương pháp giải - Xem chi tiết
Chèn điểm M: →AB=→AM+→MB,
Tính chất trung điểm →MA+→MB=→0
Lời giải chi tiết
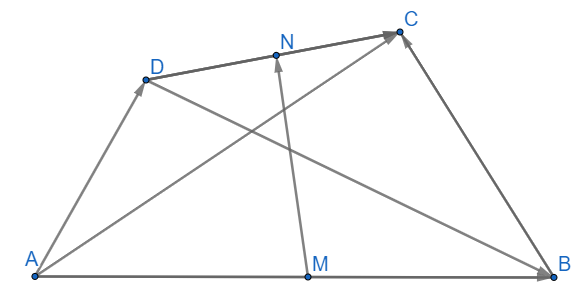
a) →AC+→BD=→AM+→MN+→NC+→BM+→MN+→ND=(→AM+→BM)+(→MN+→MN)+(→NC+→ND)=→0+2→MN+→0=2→MN (đpcm)
b) →AC+→BD=→BC+→AD
→BC+→AD=→BM+→MN+→NC+→AM+→MN+→ND
(→BM+→AM)+(→MN+→MN)+(→NC+→ND)=2→MN
Mặt khác ta có: →AC+→BD=2→MN
Suy ra →AC+→BD=→BC+→AD
Cách 2:
→AC+→BD=→BC+→AD⇔→AC−→AD=→BC−→BD⇔→DC=→DC(đpcm)

