HĐ Khám phá 5
Cho hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm tọa độ vectơ \(\overrightarrow {AB} \) theo tọa độ hai điểm A,B
Phương pháp giải:
Với \(\overrightarrow v = \left( {{v_1};{v_2}} \right),\overrightarrow w = \left( {{w_1};{w_2}} \right)\) thì \(\overrightarrow v + \overrightarrow w \) là \(\left( {{v_1} + {w_1};{v_2} + {w_2}} \right)\)
Lời giải chi tiết:
Ta có tọa độ vectơ \(\overrightarrow {OB} ,\overrightarrow {OA} \) chính là tọa độ điểm B và A
Nên ta có \(\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OA} = \left( {{x_A};{y_A}} \right)\)
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{x_B};{y_B}} \right) - \left( {{x_A};{y_A}} \right) = ({x_B} - {x_A};{y_B} - {y_A})\)
Thực hành 3
Cho \(E\left( {9;9} \right),F\left( {8; - 7} \right),G\left( {0; - 6} \right)\). Tìm tọa độ các vectơ \(\overrightarrow {FE} ,\overrightarrow {FG} ,\overrightarrow {EG} \)
Phương pháp giải:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\)
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\overrightarrow {FE} = ({x_E} - {x_F};{y_E} - {y_F}) = (9 - 8;9 - ( - 7)) = (1;16)\\\overrightarrow {FG} = ({x_G} - {x_F};{y_G} - {y_F}) = (0 - 8;( - 6) - ( - 7)) = ( - 8;1)\\\overrightarrow {EG} = ({x_G} - {x_E};{y_G} - {y_E}) = (0 - 9;( - 6) - 9) = ( - 9; - 15)\end{array}\)
HĐ Khám phá 6
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh là \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Gọi \(M\left( {{x_M};{y_M}} \right)\) là trung điểm của đoạn thẳng AB, \(G\left( {{x_G};{y_G}} \right)\) là trọng tâm của tam giác ABC
a) Biểu thị vectơ \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \)
b) Biểu thị vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \), \(\overrightarrow {OB} \) và \(\overrightarrow {OC} \)
c) Từ các kết quả trên, tìm tọa độ điểm M, G theo tọa độ của các điểm A, B, C
Phương pháp giải:
a) Sử dụng tính chất trung điểm \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\) (với M là trung điểm của đoạn thẳng AB)
b) Sử dụng tính chất trọng tâm \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\) (với G là trọng tâm của tam giác ABC)
c) Thay tọa độ các điểm vào và xác định
Lời giải chi tiết:
a) M là trung điểm của đoạn thẳng AB, áp dụng tính chất trung điểm ta có:
\(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) G là trọng tâm của tam giác ABC, áp dụng tính chất trọng tâm của tam giác ta có:
\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
c) Ta có \(\overrightarrow {OA} = \left( {{x_A};{y_A}} \right),\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OC} = \left( {{x_C};{y_C}} \right)\)
Suy ra:
\(\begin{array}{l}\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\end{array}\)
\(\begin{array}{l}
\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right) + \left( {{x_c};{y_c}} \right)} \right]\\
= \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)
\end{array}\)
Mà ta có tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ điểm M, nên ta có
Tọa độ điểm M là \(\left( {{x_M};{y_M}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm G là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Thực hành 4
Cho tam giác QRS có tọa độ các đỉnh \(Q\left( {7; - 2} \right),R( - 4;9)\) và \(S(5;8)\)
a) Tìm tọa độ trung điểm M của cạnh QS
b) Tìm tọa độ trọng tâm G của tam giác QRS
Phương pháp giải:
Tọa độ điểm M là \(\left( {\frac{{{x_Q} + {x_S}}}{2};\frac{{{y_Q} + {y_S}}}{2}} \right)\)
Tọa độ điểm G là \(\left( {\frac{{{x_Q} + {x_R} + {x_S}}}{3};\frac{{{y_Q} + {y_R} + {y_S}}}{3}} \right)\)
Lời giải chi tiết:
a) \({x_M} = \frac{{{x_Q} + {x_S}}}{2} = \frac{{7 + ( - 2)}}{2} = \frac{5}{2}; \\{y_M} = \frac{{{y_Q} + {y_S}}}{2} = \frac{{( - 2) + 8}}{2} = 3\)
Vậy \(M\left( {\frac{5}{2};3} \right)\)
b)
\({x_G} = \frac{{{x_Q} + {x_S} + {x_R}}}{3} = \frac{{7 + ( - 2) + ( - 4)}}{3} = \frac{1}{3};\\{y_M} = \frac{{{y_Q} + {y_S} + {y_R}}}{3} = \frac{{( - 2) + 8 + 9}}{3} = 5\)
Vậy \(G\left( {\frac{1}{3};5} \right)\)
HĐ Khám phá 7
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2}),\overrightarrow b = ({b_1};{b_2})\) và hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Hoàn thành các phép biến đổi sau:
a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = ...?\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right. \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = ...?\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {.?.} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} = \sqrt {.?.} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{.?.}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\) (\(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \))
Lời giải chi tiết:
a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = 0\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right.\)
\( \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = {a_1}.k{a_2} - {a_2}.k{a_1} = 0\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {{a_1}^2 + {a_2}^2} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} \)
\( = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{a_1}{b_1} + {a_2}{b_2}}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\)
Thực hành 5
Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ các đỉnh \(D(2;2),E(6;2)\) và \(F(2;6)\)
a) Tìm tọa độ điểm H là chân đường vuông cao của tam giác DEF kẻ từ D
b) Giải tam giác DEF
Phương pháp giải:
Bước 1: Tìm tọa độ các vectơ \(\overrightarrow {DH} ,\overrightarrow {EF} \)
Bước 2: Dựa vào ứng dụng tọa độ của các phép toán vectơ (tính chất vuông góc)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {EF} = \left( { - 2;4} \right)\)
Gọi tọa độ điểm H là \(\left( {x;y} \right)\) ta có \(\overrightarrow {DH} = \left( {x - 2;y - 2} \right),\overrightarrow {EH} = \left( {x - 6;y - 2} \right)\)
H là chân đường cao nên \(\overrightarrow {DH} \bot \overrightarrow {EF} \)
\(\begin{array}{l}\overrightarrow {DH} \bot \overrightarrow {EF} \Leftrightarrow \left( {x - 2} \right).\left( { - 2} \right) + \left( {y - 2} \right).4 = 0\\ \Leftrightarrow - 2x + 4y - 4 = 0\end{array}\) (1)
Hai vectơ \(\overrightarrow {EH} ,\overrightarrow {EF} \) cùng phương
\( \Leftrightarrow \left( {x - 6} \right).( - 2) - \left( {y - 2} \right).4 = 0 \Leftrightarrow - 2x - 4y + 20 = 0\) (2)
Từ (1) và (2) ta có hệ phương trình
\(\left\{ \begin{array}{l} - 2x + 4y - 4 = 0\\ - 2x - 4y + 20 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\)
Vậy \(H(4;3)\)
b) Ta có: \(\overrightarrow {DE} = (4;0),\overrightarrow {DF} = (0;4),\overrightarrow {EF} = ( - 4;4)\)
Suy ra: \(DE = \left| {\overrightarrow {DE} } \right| = \sqrt {{4^2} + {0^2}} = 4,DF = \left| {\overrightarrow {DF} } \right| = \sqrt {{0^2} + {4^2}} = 4\)
\(EF = \left| {\overrightarrow {EF} } \right| = \sqrt {{{( - 4)}^2} + {4^2}} = 4\sqrt 2 \)
\(\begin{array}{l}\cos D = \cos \left( {\overrightarrow {DE} ,\overrightarrow {DF} } \right) = \frac{{\overrightarrow {DE} .\overrightarrow {DF} }}{{DE.DF}} = \frac{{4.0 + 0.4}}{{4.4}} = 0 \Rightarrow \widehat D = 90^\circ \\\cos E = \cos \left( {\overrightarrow {ED} ,\overrightarrow {EF} } \right) = \frac{{\overrightarrow {ED} .\overrightarrow {EF} }}{{ED.EF}} = \frac{{\left( { - 4} \right).\left( { - 4} \right) + 0.4}}{{4.4\sqrt 2 }} = \frac{{\sqrt 2 }}{2} \Rightarrow \widehat E = 45^\circ \\\widehat F = 180^\circ - \widehat D - \widehat E = 180^\circ - 90^\circ - 45^\circ = 45^\circ \end{array}\)
Vận dụng 3
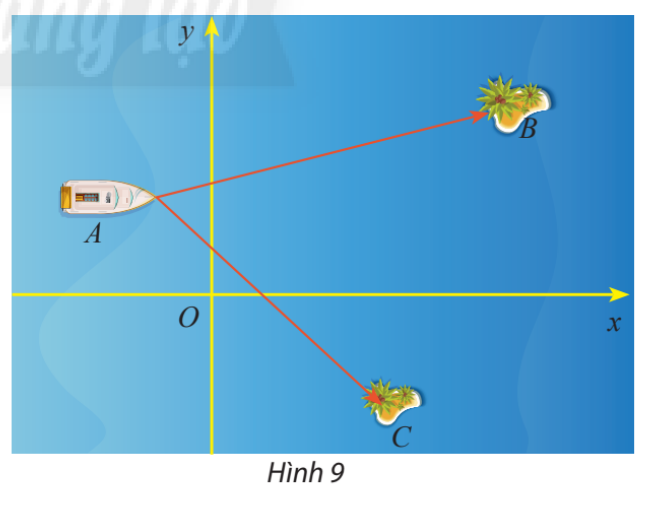
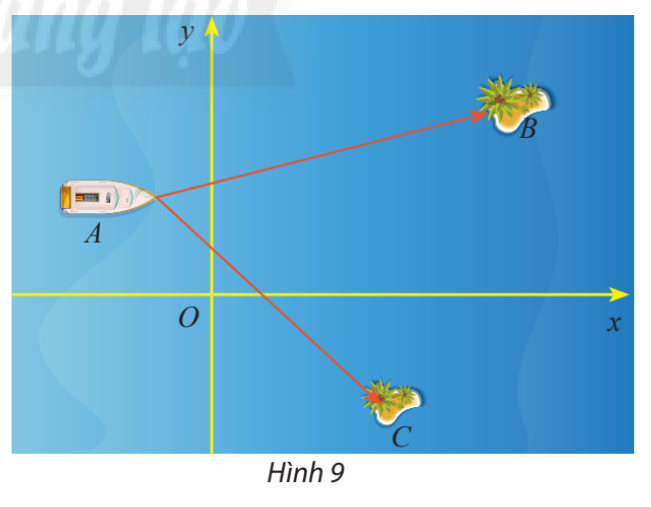
Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ \(B\left( {50;30} \right)\) và \(C\left( {32; - 23} \right)\). Một con tàu đang neo đậu tại điểm \(A\left( { - 10;20} \right)\)
a) Tính số đo của \(\widehat {BAC}\)
b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1km. Tính khoảng cách từ con tàu đến mỗi hòn đảo
Phương pháp giải:
Bước 1: Xác định tọa độ các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \)
Bước 2:
a) \(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} \)
b) \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {(x_B - x_A)^2+(y_B-y_A)^2}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \left( {60;10} \right),\overrightarrow {AC} = \left( {42; - 43} \right),\overrightarrow {BC} = \left( { - 18; - 53} \right)\)
\(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{60.42 + 10.( - 43)}}{{\sqrt {{{60}^2} + {{10}^2}} .\sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} }} \simeq 0,572 \Rightarrow \widehat {BAC} \approx 55^\circ 8'\)
b)
Khoảng cách từ tàu đến đảo B là \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{60}^2} + {{10}^2}} = 10\sqrt {37} \) (km)
Khoảng cách từ tàu đến đảo B là \(AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} = \sqrt {3613} \) (km)
