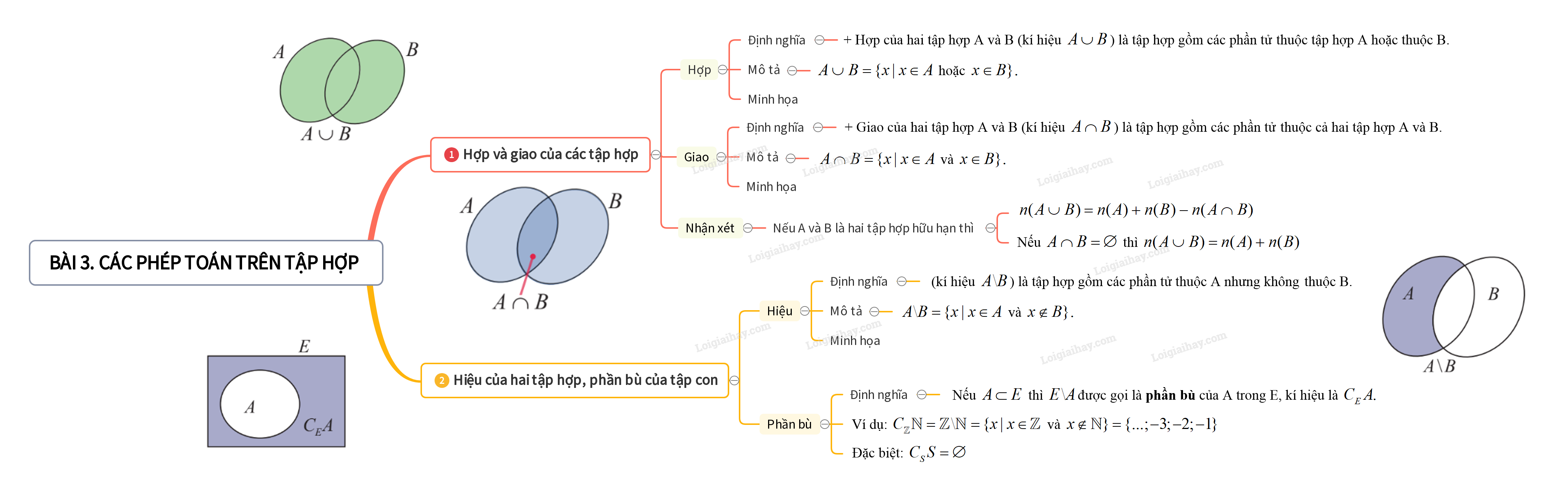
1. Hợp và giao của các tập hợp
+ Hợp của hai tập hợp A và B (kí hiệu \(A \cup B\)) là tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc T.
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} .\)
+ Giao của hai tập hợp A và B (kí hiệu \(A \cap B\)) là tập hợp gồm các phần tử thuộc cả hai tập hợp A và B.
\(A \cap B = \{ x|x \in A\) và \(x \in B\} .\)

+ Nhận xét: Nếu A và B là hai tập hợp hữu hạn thì
\(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)
Nếu \(A \cap B = \emptyset \) thì \(n(A \cup B) = n(A) + n(B)\)
2. Hiệu của hai tập hợp, phần bù của tập con
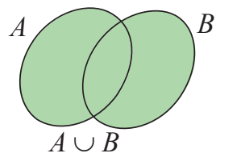
Hiệu của hai tập hợp A và B (kí hiệu \(A{\rm{\backslash }}B\)) là tập hợp gồm các phần tử thuộc A nhưng không thuộc B.
\(A{\rm{\backslash }}B = \{ x|x \in A\) và \(x \notin B\} .\)
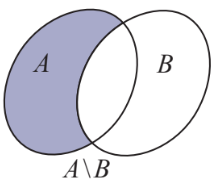
Nếu \(A \subset E\) thì \(E{\rm{\backslash }}A\)được gọi là phần bù của A trong E, kí hiệu là \({C_E}A.\)
Ví dụ: \({C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z}\) và \(x \notin \mathbb{N}\} = \{ ...; - 3; - 2; - 1\} \)
Đặc biệt: \({C_S}S = \emptyset \)