Đề bài
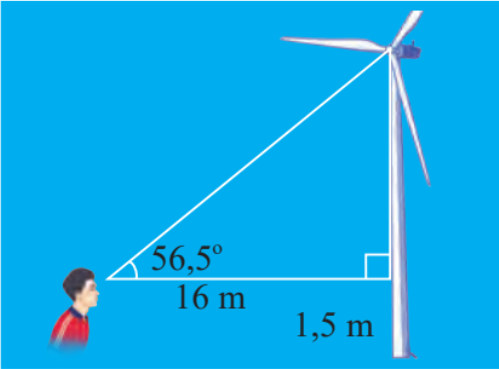
Một người đứng cách thân một các quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng \(56,{5^o}\) (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 1,5m.
Phương pháp giải - Xem chi tiết
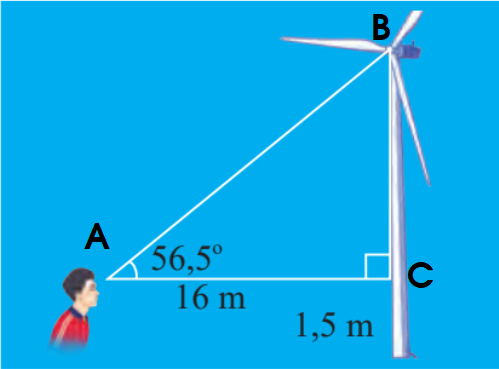
Kí hiệu các điểm A, B, C như hình dưới.
Cách 1:
Tính góc B rồi áp dụng định lí sin để tính BC: \(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)
Cách 2:
\(\tan A = \frac{{BC}}{{AC}} \Rightarrow BC = AC.\tan A\)
Lời giải chi tiết
Kí hiệu các điểm A, B, C như hình dưới.

Cách 1:
Ta có: \(\widehat B = {90^o} - 56,{5^o} = 33,{5^o}\)
Áp dụng định lí sin, ta có: \(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow BC = \sin A.\frac{{AC}}{{\sin B}} = \sin 56,{5^o}.\frac{{16}}{{\sin 33,{5^o}}} \approx 24,2\;(m)\)
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là \(24,2 + 1,5 = 15,7(m)\)
Cách 2:
\(\tan A = \frac{{BC}}{{AC}} \Rightarrow BC = AC.\tan A = 16.\tan 56,{5^o} \approx 24,2\)
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là \(24,2 + 1,5 = 15,7(m)\)

