Đề bài
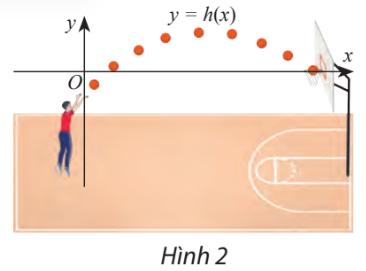
Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số \(h\left( x \right) = - 0,1{x^2} + x - 1\). Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ và ngang vành rổ? Làm tròn các kết quả đến hàng phần mười.
Phương pháp giải - Xem chi tiết
Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Xác định nghiệm của \(h\left( x \right)\) (nếu có) \(x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\)
Bước 3: Lập bảng xét dấu
Bước 4: Dựa vào bảng xét dấu đưa ra các khoảng theo yêu cầu
+) Khoảng mà \(h\left( x \right) > 0\) là khoảng bóng nằm cao hơn vành rổ
+) Khoảng mà \(h\left( x \right) < 0\) là khoảng bóng nằm thấp hơn vành rổ
+) Khoảng mà \(h\left( x \right) = 0\) là khoảng bóng nằm ngang vành rổ
Lời giải chi tiết
\(h\left( x \right) = - 0,1{x^2} + x - 1\) có \(\Delta = \frac{3}{5} > 0\), có hai nghiệm phân biệt là \({x_1} = 5 - \sqrt {15} ;{x_2} = 5 + \sqrt {15} \)
Ta có bảng xét dấu như sau
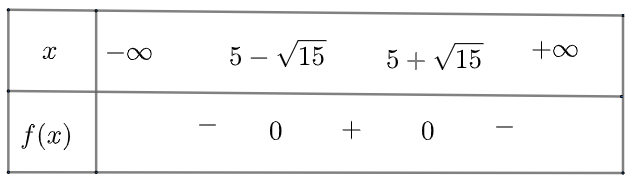
Vậy khoảng bóng nằm trên vành rổ là \(x \in \left( {1,2;8,9} \right)\)mét
khoảng bóng nằm dưới vành rổ là \(x \in \left( { - \infty ;1,2} \right) \cup \left( {8,9; + \infty } \right)\) mét
khoảng bóng nằm ngang vành rổ là \(x \simeq \left\{ {1,2;8,9} \right\}\)

