Đề bài
Xét dấu của các tam thức bậc hai sau:
a) \(f\left( x \right) = 6{x^2} + 41x + 44\)
b) \(g\left( x \right) = - 3{x^2} + x - 1\)
c) \(h\left( x \right) = 9{x^2} + 12x + 4\)
Phương pháp giải - Xem chi tiết
Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Xác định nghiệm của \(f\left( x \right)\)nếu có
Bước 3: Các định dấu của hệ số a
Bước 4: Xác định dấu của \(f\left( x \right)\)
Lời giải chi tiết
a) \(f\left( x \right) = 6{x^2} + 41x + 44\) có \(\Delta = 625 > 0\), có hai nghiệm phân biệt là \({x_1} = - \frac{{11}}{2},{x_2} = - \frac{4}{3}\) và có \(a = 6 > 0\)
Ta có bảng xét dấu \(f\left( x \right)\)như sau:
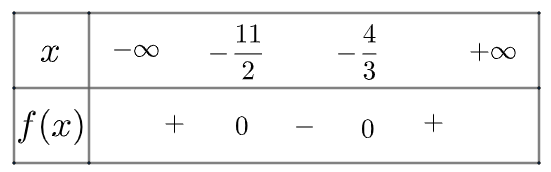
Vậy \(f\left( x \right)\) dương trong khoảng \(\left( { - \infty ; - \frac{{11}}{2}} \right) \cup \left( { - \frac{4}{3}; + \infty } \right)\) và âm trong khoảng \(\left( { - \frac{{11}}{2}; - \frac{4}{3}} \right)\)
b) \(g\left( x \right) = - 3{x^2} + x - 1\) có \(\Delta = - 11 < 0\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau
Vậy \(g\left( x \right)\)luôn âm với mọi \(x \in \mathbb{R}\)
c) \(h\left( x \right) = 9{x^2} + 12x + 4\) có \(\Delta = 0\), có nghiệm kép là \({x_1} = {x_2} = - \frac{2}{3}\) và có \(a = 9 > 0\)
Ta có bảng xét dấu của \(h\left( x \right)\) như sau:
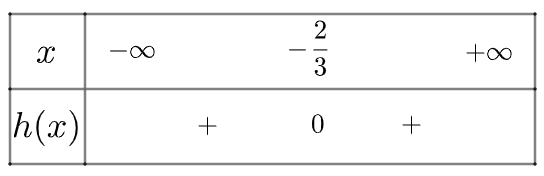
Vậy \(h\left( x \right)\) luôn dương khi \(x \ne - \frac{2}{3}\)
