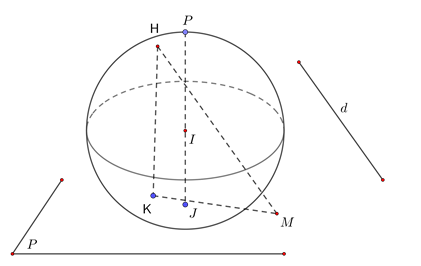
Trong không gian tọa độ $O x y z$, cho 5 điểm \(A(1;0;0),B( - 1;1;0),C(0; - 1;0\) \(D(0;1;0),E(0;3;0),M\) là điểm thay đổi trên mặt cầu \((S):{x^2} + {(y - 1)^2} + {z^2} = 1\). Giá trị lớn nhất của biểu thức \(P = 2|\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} | + 3|\overrightarrow {MD} + \overrightarrow {ME} |\) là
Bước 1: Gọi điểm \(I\) thỏa mãn \(\vec A + \overrightarrow {IB} + \overrightarrow {IC} = \vec 0\), điểm \(J\) thỏa mãn \(\overrightarrow {JD} + \overrightarrow {JE} = \vec 0\). Biểu diễn P theo \(|\overrightarrow {MI} |\) và \(|\overrightarrow {MJ} |\)
\((S)\) có tâm \(T(0;1;0)\) và bán kính \(R = 1\).
Gọi điểm \(I\) thỏa mãn \(\vec A + \overrightarrow {IB} + \overrightarrow {IC} = \vec 0\)\( \Rightarrow I(0;0;0)\)
Điểm \(J\) thỏa mãn \(\overrightarrow {JD} + \overrightarrow {JE} = \vec 0\)\( \Rightarrow J(0;2;0)\)
Ta có: \(P = 2|\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} |\)\( + 3|\overrightarrow {MD} + \overrightarrow {ME} |\)
\( = 2|3\overrightarrow {MI} | + 3|2\overrightarrow {MJ} |\)\( = 6|\overrightarrow {MI} | + 6|\overrightarrow {MJ} |\)
Bước 2: Gọi \(F\) là điểm thỏa mãn \(\overrightarrow {FI} + \overrightarrow {FJ} = \vec 0\). Tìm max\(P\).
Gọi \(F\) là điểm thỏa mãn \(\overrightarrow {FI} + \overrightarrow {FJ} = \vec 0\)\( \Rightarrow F(0;1;0) \equiv T\).
\(\left. {P \le \sqrt {72\left( {|\overrightarrow {MI} {|^2} + |\overrightarrow {MJ} {|^2}} \right.} } \right)\)\( = \sqrt {72\left( {{{\overrightarrow {MI} }^2} + {{\overrightarrow {MJ} }^2}} \right)} \)\( = \sqrt {72\left( {F{I^2} + F{J^2} + 2M{F^2}} \right)} \)
Như vậy \({\rm{P}}\) lớn nhất khi $M F$ lớn nhất. \({\rm{M}}\) thuộc \((S)\) nên $M F$ lớn nhất khi \(MF = R = 1\). Vậy \(P \le \sqrt {72(1 + 1 + 2)} = 12\sqrt 2 \).
Trong không gian \(Oxyz\), cho điểm \(A\left( {1; - 2;3} \right)\) và đường thẳng $d$ có phương trình: \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + t\\z = - 3 - t\end{array} \right.\left( {t \in \mathbb{R}} \right)\). Mặt cầu \(\left( S \right)\) có tâm $A$ và tiếp xúc với đường thẳng $d$ có bán kính là
Phương trình mặt phẳng $\left( P \right)$ đi qua $A$ và vuông góc với $d$ là :
\(2\left( {x - 1} \right) + 1\left( {y + 2} \right) - 1\left( {z - 3} \right) = 0 \Leftrightarrow 2x + y - z + 3 = 0\).
Gọi $H$ là hình chiếu của $A$ lên $\left( P \right)$. Khi đó : \(H = d \cap \left( P \right) \Leftrightarrow \left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + t\\z = - 3 - t\\2x + y - z + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - 1\\x = - 3\\y = 1\\z = - 2\end{array} \right. \Rightarrow H( - 3;1; - 2)\)
\(R = AH = \sqrt {{{\left( { - 3 - 1} \right)}^2} + {{\left( {1 + 2} \right)}^2} + {{\left( { - 2 - 3} \right)}^2}} = 5\sqrt 2 \).
Phương trình mặt cầu có tâm \(I\left( {1; - 2;3} \right)\) và tiếp xúc với trục \(Oy\) là
Vì mặt cầu tiếp xúc với trục \(Oy:\,\,\left\{ \begin{array}{l}x = 0\\y = t\\z = 0\end{array} \right.\) nên mặt cầu có bán kính \(R = d\left( {I;Oy} \right)\)
Ta có: \(\overrightarrow {OI} = \left( {1; - 2;3} \right),\overrightarrow j = \left( {0;1;0} \right) \Rightarrow \left[ {\overrightarrow {OI} ,\overrightarrow j } \right] = \left( { - 3;0;1} \right)\) nên \(R = d\left( {I;Oy} \right)\)\( = \dfrac{{\left| {\left[ {\overrightarrow {OI} ;\overrightarrow j } \right]} \right|}}{{\left| {\overrightarrow j } \right|}} = \sqrt {10} \)
Phương trình mặt cầu là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 10\)
\( \Leftrightarrow {x^2} + {y^2} + {z^2} - 2x + 4y - 6z + 4 = 0\)
Đề thi THPT QG 2019 – mã đề 104
Trong không gian \(Oxyz\) cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {\left( {z - 1} \right)^2} = 5\). Có tất cả bao nhiêu điểm \(A\left( {a;b;c} \right)\) (a, b, c là các số nguyên) thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho có ít nhất hai tiếp tuyến của \(\left( S \right)\) đi qua A và hai tiếp tuyến đó vuông góc với nhau ?
Mặt cầu \(\left( S \right):{x^2} + {y^2} + {\left( {z - 1} \right)^2} = 5\) có tâm \(I\left( {0;0;1} \right)\), bán kính \(R = \sqrt 5 \).
Do \(A\left( {a;b;c} \right) \in Oxy \Rightarrow c = 0 \Rightarrow A\left( {x;y;0} \right)\).
Để từ A kẻ được ít nhất 2 tiếp tuyến vuông góc với nhau đến mặt cầu \(\left( S \right)\) thì \(R \le IA \le R\sqrt 2 \).
\( \Leftrightarrow \sqrt 5 \le \sqrt {{x^2} + {y^2} + {1^2}} \le \sqrt {10} \)\( \Leftrightarrow 4 \le {x^2} + {y^2} \le 9\), do đó tập hợp các điểm A là hình vành khăn (tính cả biên) giữa hai đường tròn \({x^2} + {y^2} = 4\) và \({x^2} + {y^2} = 9\).
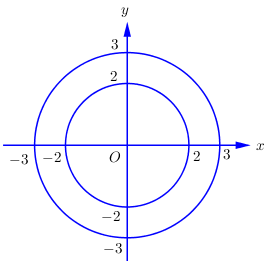
Ta có \(4 \le {x^2} + {y^2} \le 9\). Mà \(x,\,\,y \in \mathbb{Z} \Rightarrow {x^2} \le 9 \Rightarrow x \in \left\{ {0; \pm 1; \pm 2; \pm 3} \right\}\).
Ta có bảng giá trị:

Vậy có 20 điểm thỏa mãn yêu cầu bài toán.
Trong không gian với hệ tọa độ \(Oxyz\) cho mặt cầu \(\left( S \right)\) có phương trình \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 50\). Trong số các đường thẳng sau, mặt cầu \(\left( S \right)\) tiếp xúc với đường thẳng nào?
Mặt cầu \(\left( S \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 50\) có tâm \(I\left( {1; - 2;3} \right)\), bán kính \(R = \sqrt {50} = 5\sqrt 2 \).
Đường thẳng \(d\) tiếp xúc với mặt cầu \(\left( S \right)\) khi và chỉ khi \(d\left( {I;d} \right) = R\).
Thử lần lượt các đáp án ta có:
\(d\left( {I;Ox} \right) = \sqrt {y_I^2 + z_I^2} = \sqrt {{{\left( { - 2} \right)}^2} + {3^2}} = \sqrt {13} \ne R\), do đó loại đáp án B.
\(d\left( {I;Oy} \right) = \sqrt {x_I^2 + z_I^2} = \sqrt {{1^2} + {3^2}} = \sqrt {10} \ne R\), do đó loại đáp án C.
\(d\left( {I;Oz} \right) = \sqrt {x_I^2 + y_I^2} = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \ne R\), do đó loại đáp án D.
Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(I\left( 3;4;-\,2 \right).\) Lập phương trình mặt cầu tâm \(I\) và tiếp xúc với trục \(Oz.\)
Phương trình trục \(Oz:\ \ \left\{ \begin{align} & x=0 \\ & y=0 \\ & z=t \\ \end{align} \right.,\ \ \overrightarrow{{{u}_{Oz}}}=\left( 0;\ 1;\ 1 \right).\)
Ta có : \(\overrightarrow{OI}=\left( 3;\ 4;\ -2 \right)\Rightarrow \left[ \overrightarrow{OI},\ \overrightarrow{{{u}_{Oz}}} \right]=\left( 4;-3;\ 0 \right).\)
Khoảng cách từ tâm \(I\,\,\xrightarrow{{}}\,\,Oz\) là \(d\left( I;\left( Oz \right) \right)=\frac{\left| \left[ \overrightarrow{OI},\ \overrightarrow{{{u}_{Oz}}} \right] \right|}{\left| \overrightarrow{{{u}_{Oz}}} \right|}=\sqrt{{{3}^{2}}+{{4}^{2}}}=5=R.\)
Vì \(\left( S \right)\) tiếp xúc với trục \(Oz\)\(\Rightarrow \) Phương trình cần tìm là \(\left( S \right):{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}+{{\left( z+2 \right)}^{2}}=25.\)
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right):\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-4x+10y-2z-6=0\). Cho \(m \) là số thực thỏa mãn giao tuyến của hai mặt phẳng \(y=m\) và \(x+z-3=0\) tiếp xúc với mặt cầu \(\left( S \right)\). Tích tất cả các giá trị mà \(m\) có thể nhận được bằng:
Mặt cầu \(\left( S \right)\) có tâm \(I\left( 2;-5;1 \right)\) bán kính \(R=\sqrt{4+25+1+6}=6\)
Giao tuyến của hai mặt phẳng \(y=m\) và \(x+z-3=0\) là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}
y = m\\
x + z - 3 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = t\\
y = m\\
z = 3 - t
\end{array} \right.\,\,\left( d \right) \)
\(\Rightarrow \) Đường thẳng (d) đi qua \(M\left( 0;m;3 \right)\) và có 1 VTCP là \(\overrightarrow{u}=\left( 1;0;-1 \right)\)
Ta có:
$\begin{array}{l}
\overrightarrow {IM} = \left( { - 2;m + 5;2} \right),\overrightarrow u = \left( {1;0; - 1} \right)\\
\Rightarrow \left[ {\overrightarrow {IM} ,\overrightarrow u } \right] = \left( {\left| \begin{array}{l}
m + 5\,\,\,\,\,2\\
0\,\,\,\,\,\,\,\,\,\, - 1
\end{array} \right|,\left| \begin{array}{l}
2\,\,\,\,\,\, - 2\\
- 1\,\,\,\,\,\,\,1
\end{array} \right|,\left| \begin{array}{l}
- 2\,\,\,\,m + 5\\
1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0
\end{array} \right|} \right)\\
= \left( { - m - 5;0; - m - 5} \right)\\
\Rightarrow \left| {\left[ {\overrightarrow {IM} ,\overrightarrow u } \right]} \right| = \sqrt {{{\left( { - m - 5} \right)}^2} + {0^2} + {{\left( { - m - 5} \right)}^2}} \\
= \sqrt {{{\left( {m + 5} \right)}^2} + {{\left( {m + 5} \right)}^2}} = \sqrt {2{{\left( {m + 5} \right)}^2}} = \left| {m + 5} \right|\sqrt 2
\end{array}$
Đường thẳng (d) tiếp xúc với mặt cầu \(\left( S \right)\Leftrightarrow d\left( I;d \right)=R\)
\( \Rightarrow \frac{{\left| {\left[ {\overrightarrow {IM} ;\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = R \Leftrightarrow \frac{{\left| {m + 5} \right|\sqrt 2 }}{{\sqrt 2 }} = 6 \Leftrightarrow \left[ \begin{array}{l}
m + 5 = 6\\
m + 5 = - 6
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
m = 1\\
m = - 11
\end{array} \right.\)
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\frac{x-1}{1}=\frac{y+1}{1}=\frac{z-m}{2}\) và mặt cầu \((S):{{(x-1)}^{2}}+{{(y-1)}^{2}}+{{(z-2)}^{2}}=9.\) Tìm \(m\) để đường thẳng \(d\) cắt mặt cầu \((S)\) tại hai điểm phân biệt \(E,\,\,F\) sao cho độ dài đoạn thẳng \(EF\) lớn nhất
Ta có \(E{{F}_{\max }}\Leftrightarrow d{{\left( I;\left( d \right) \right)}_{\min }}=\frac{\left| \left[ \overrightarrow{I{{M}_{0}}};\overrightarrow{{{u}_{d}}} \right] \right|}{\left| \overrightarrow{{{u}_{d}}} \right|}{{\ }_{\min }}\) (trong đó điểm \({{M}_{0}}\left( 1;-1;m \right)\))
Ta có: \(d\left( I;\left( d \right) \right)=\frac{\left| \left[ \overrightarrow{I{{M}_{0}}};\overrightarrow{{{u}_{d}}} \right] \right|}{\left| \overrightarrow{{{u}_{d}}} \right|}\ =\frac{\sqrt{{{\left( m+2 \right)}^{2}}+{{\left( m-2 \right)}^{2}}+4}}{\sqrt{1+1+4}}=\frac{\sqrt{2{{m}^{2}}+12}}{\sqrt{6}}\)
Vì \(2{{m}^{2}}\ge 0\) suy ra \(d\left( I;\left( d \right) \right)\le \frac{\sqrt{12}}{\sqrt{6}}=\sqrt{2}\Rightarrow \,\,{{d}_{\min }}=\sqrt{2}<R=3\) khi \(m=0.\)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \(\left( S \right):\,\,{{x}^{2}}+{{\left( y+2 \right)}^{2}}+{{z}^{2}}=5\). Tìm tất cả các giá trị thực của tham số m để đường thẳng \(\Delta :\,\,\frac{x-1}{2}=\frac{y+m}{1}=\frac{z-2m}{-3}\) cắt \(\left( S \right)\) tại hai điểm phân biệt A, B sao cho A, B có độ dài AB lớn nhất.
Mặt cầu (S) có tâm \(I\left( 0;-2;0 \right)\) và bán kính \(R=\sqrt{5}\).
Dễ thấy \(I\notin \Delta \).
Ta có: \({{\overrightarrow{u}}_{\Delta }}=\left( 2;1;-3 \right),\,\,M\left( 1;-m;2m \right)\in \Delta ,\,\,\overrightarrow{IM}=\left( 1;2-m;2m \right)\)
\(\begin{align} & \Rightarrow \left[ \overrightarrow{IM};{{\overrightarrow{u}}_{\Delta }} \right]=\left( m-6;4m+3;2m-3 \right) \\ & \Rightarrow d\left( I;\Delta \right)=\frac{\left| \left[ \overrightarrow{IM};{{\overrightarrow{u}}_{\Delta }} \right] \right|}{\left| {{\overrightarrow{u}}_{\Delta }} \right|}=\frac{\sqrt{21{{m}^{2}}+54}}{\sqrt{14}} \\ \end{align}\)
Để AB lớn nhất \(\Leftrightarrow d{{\left( I;\Delta \right)}_{\min }}\Leftrightarrow {{\left( 21{{m}^{2}}+54 \right)}_{\min }}\Leftrightarrow m=0\)
Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(I\left( 3;4;-\,2 \right).\) Lập phương trình mặt cầu tâm \(I\) và tiếp xúc với trục \(Oz.\)
Phương trình trục \(Oz:\ \ \left\{ \begin{align} & x=0 \\ & y=0 \\ & z=t \\ \end{align} \right.,\ \ \overrightarrow{{{u}_{Oz}}}=\left( 0;\ 0;\ 1 \right).\)
Ta có : \(\overrightarrow{OI}=\left( 3;\ 4;\ -2 \right)\Rightarrow \left[ \overrightarrow{OI},\ \overrightarrow{{{u}_{Oz}}} \right]=\left( 4;-3;\ 0 \right).\)
Khoảng cách từ tâm \(I\,\,\xrightarrow{{}}\,\,Oz\) là \(d\left( I;\left( Oz \right) \right)=\frac{\left| \left[ \overrightarrow{OI},\ \overrightarrow{{{u}_{Oz}}} \right] \right|}{\left| \overrightarrow{{{u}_{Oz}}} \right|}=\sqrt{{{3}^{2}}+{{4}^{2}}}=5=R.\)
Vì \(\left( S \right)\) tiếp xúc với trục \(Oz\)\(\Rightarrow \) Phương trình cần tìm là \(\left( S \right):{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}+{{\left( z+2 \right)}^{2}}=25.\)
Có bao nhiêu mặt cầu \(\left( S \right)\) có tâm thuộc đường thẳng \(\Delta :\frac{x-3}{2}=\frac{y-1}{-1}=\frac{z-1}{-2}\) đồng thời tiếp xúc với hai mặt phẳng \(\left( {{\alpha _1}} \right):2x + 2y + z - 6 = 0\) và \(\left( {{\alpha }_{2}} \right):x-2y+2z=0\)
Phương trình tham số của đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 3 + 2t\\y = 1 - t\\z = 1 - 2t\end{array} \right.\)
Gọi tâm \(I \in \Delta \)\( \Rightarrow I\left( {3 + 2t;1 - t;1 - 2t} \right)\)
Vì mặt cầu \(\left( S \right)\) đồng thời tiếp xúc với hai mặt phẳng \(\left( {{\alpha }_{1}} \right)\) và \(\left( {{\alpha _2}} \right)\) nên \(d\left( I,\left( {{\alpha }_{1}} \right) \right)\)\(=d\left( I,\left( {{\alpha }_{2}} \right) \right)\)
\( \Leftrightarrow \frac{{\left| {2\left( {3 + 2t} \right) + 2\left( {1 - t} \right) + 1 - 2t - 6} \right|}}{{\sqrt {{2^2} + {2^2} + {1^1}} }}\)\( = \frac{{\left| {3 + 2t - 2\left( {1 - t} \right) + 2\left( {1 - 2t} \right)} \right|}}{{\sqrt {{2^2} + {2^2} + {1^1}} }}\)\( \Leftrightarrow \frac{{\left| 3 \right|}}{3} = \frac{{\left| 3 \right|}}{3}\) (luôn đúng).
Vậy có vô số mặt phẳng tiếp xúc với cả hai mặt phẳng.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu \(\left( S \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 25\). Đường thẳng d cắt mặt cầu \(\left( S \right)\) tại hai điểm A, B. Biết tiếp diện của \(\left( S \right)\) tại A và B vuông góc. Tính độ dài AB.
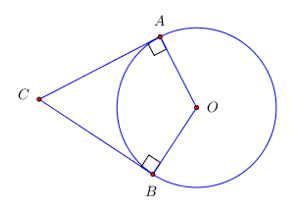
Tiếp diện của \(\left( S \right)\) tại A và B vuông góc với nhau khi và chỉ khi OACB là hình vuông \( \Rightarrow AB = R\sqrt 2 = 5\sqrt 2 \).
Trong không gian \(Oxyz,\) cho mặt cầu \((S):{{(x-1)}^{2}}+{{(y-2)}^{2}}+{{(z+1)}^{2}}=6,\) tiếp xúc với hai mặt phẳng \((P):x+y+2z\,+\,5=0,\,\,(Q):2x-y+z\,-\,5=0\) lần lượt tại các tiếp điểm \(A,\,\,B.\) Độ dài đoạn thẳng \(AB\) là
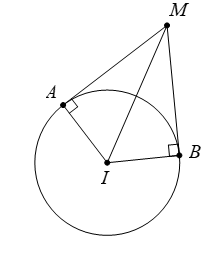
Xét \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=6\) có tâm \(I\left( 1;2;-\,1 \right),\) bán kính \(R=\sqrt{6}.\)
Gọi \(M\) là giao điểm của \(\left( P \right)\) và \(\left( Q \right)\) sao cho \(MAIB\) đồng phẳng.
Ta có \(\cos \widehat{AMB}=\cos \widehat{\left( P \right);\left( Q \right)}=\frac{\left| {{{\vec{n}}}_{\left( P \right)}}.{{{\vec{n}}}_{\left( Q \right)}} \right|}{\left| {{{\vec{n}}}_{\left( P \right)}} \right|.\left| {{{\vec{n}}}_{\left( Q \right)}} \right|}=\frac{1}{2}\Rightarrow \,\,\widehat{AMB}={{60}^{0}}\Rightarrow \,\,\widehat{AIB}={{120}^{0}}.\)
Tam giác \(IAB\) cân tại \(I,\) có \(AB=\sqrt{I{{A}^{2}}+I{{B}^{2}}-2.IA.IB.\cos \widehat{AIB}}=3\sqrt{2}.\)
Trong không gian \(Oxyz,\) mặt phẳng \(\left( P \right):\ 2x+6y+z-3=0\) cắt trục \(Oz\) và đường thẳng \(d:\ \frac{x-5}{1}=\frac{y}{2}=\frac{z-6}{-1}\) lần lượt tại \(A\) và \(B\). Phương trình mặt cầu đường kính \(AB\) là:
Phương trình trục \(Oz:\ \left\{ \begin{align} & x=0 \\ & y=0 \\ & z=t \\ \end{align} \right..\ \ \ A\in Oz\Rightarrow A\left( 0;\ 0;\ t \right).\)
Có \(\left( P \right)\cap Oz=\left\{ A \right\}\Rightarrow 2.0+6.0+t-3=0\Leftrightarrow t=3\Rightarrow A\left( 0;\ 0;\ 3 \right).\) \(d:\ \left\{ \begin{align} & x=5+t' \\ & y=2t' \\ & z=6-t' \\ \end{align} \right..\ \ B\in d\Rightarrow B\left( 5+t';2t';6-t' \right).\) Có \(\left( P \right)\cap d=\left\{ B \right\}\Rightarrow 2\left( 5+t' \right)+6.2t'+6-t'-3=0\Leftrightarrow t'=-1\Rightarrow B\left( 4;-2;7 \right).\)
Gọi \(I\) là trung điểm của \(AB\Rightarrow I\left( 2;\ -1;\ 5 \right).\)
Có \(\overrightarrow{AB}=\left( 4;-2;\ 4 \right)\Rightarrow AB=\sqrt{36}=6\Rightarrow IA=R=\frac{AB}{2}=3.\)
Vậy đường tròn đường kính AB là: \({{\left( x-2 \right)}^{2}}+{{\left( y+1 \right)}^{2}}+{{\left( z-5 \right)}^{2}}=9.\)
Trong không gian với hệ tọa độ Oxyz, cho điểm \(I(1;-2;3)\). Phương trình mặt cầu tâm $I$ và tiếp xúc với trục $Oy$ là:
Gọi E là hình chiếu của I trên Oy \(\Rightarrow E\left( 0;-2;0 \right)\)
Suy ra bán kính mặt cầu tâm I và tiếp xúc với trục Oy là:
\(R=IE\)\(=\sqrt{{{\left( 1-0 \right)}^{2}}+{{\left( -2+2 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}\)\(=\sqrt{10}\)
Vậy phương trình mặt cầu tâm $I$ và tiếp xúc với trục Oy là:\(\ {{(x-1)}^{2}}+{{(y+2)}^{2}}+{{(z-3)}^{2}}=10.\)
Trong không gian Oxyz, cho 3 điểm \(A\left( 6;0;0 \right);\,\,B\left( 0;6;0 \right);\,\,C\left( 0;0;6 \right)\). Hai mặt cầu có phương trình \(\left( {{S}_{1}} \right):\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-2y+1=0\) và \(\left( {{S}_{2}} \right):\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x+2y+2z+1=0\) cắt nhau theo đường tròn (C). Hỏi có bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa (C) và tiếp xúc với ba đường thẳng AB, BC, CA?
Mặt cầu \(\left( {{S}_{1}} \right)\) có tâm \({{I}_{1}}\left( 1;1;0 \right)\), mặt cầu \(\left( {{S}_{2}} \right)\) có tâm \({{I}_{2}}\left( 4;-1;-1 \right)\).
Dễ thấy điểm \(M\left( 1;1;1 \right)\) thuộc cả hai mặt cầu \(\Rightarrow M\in \left( P \right)\,\,\,\left( 1 \right)\).
Mặt phẳng (P) chứa (C) vuông góc với \({{I}_{1}}{{I}_{2}}\) và đi qua M. Do đó phương trình mặt phẳng (P) là:
\(3\left( x-1 \right)-2\left( y-1 \right)-\left( z-1 \right)=0\Leftrightarrow 3x-2y-z=0\).
Gọi K là tâm của mặt cầu cần tìm ta có \(K\in \left( P \right)\). Gọi A’; B’; C’ lần lượt là hình chiếu của K trên AB, BC, CA ta có \(KA'=KB'=KC'\).
Gọi K’ là hình chiếu của K trên (ABC) ta chứng minh được \(K'A\bot AB;\,\,K'B\bot BC;\,\,K'C\bot CA\) và \(K'A'=K'B'=K'C'\Rightarrow K'\) là tâm đường tròn nội tiếp tam giác ABC. Mà tam giác ABC đều \(\Rightarrow K'\) là trọng tâm của tam giác ABC \(\Rightarrow K'\left( 2;2;2 \right)\).
Phương trình mặt phẳng (ABC): \(\frac{x}{6}+\frac{y}{6}+\frac{z}{6}=1\Leftrightarrow x+y+z=6\).
\(\Rightarrow \) Phương trình đường thẳng đi qua K’ và vuông góc với (ABC) là: \(d:\,\,\frac{x-2}{1}=\frac{y-2}{1}=\frac{z-2}{1}\Rightarrow K\in d\,\,\,\left( 2 \right)\)
Từ (1) và (2) \(\Rightarrow K=\left( P \right)\cap d\Rightarrow K\left( t+2;t+2;t+2 \right)\)
Thay vào phương tình mặt phẳng (P) \(\Rightarrow 3\left( t+2 \right)-2\left( t+2 \right)-\left( t+2 \right)=0\Rightarrow \) Phương trình có vô số nghiệm.
Vậy có vô số điểm K thỏa mãn yêu cầu bài toán.
Trong không gian Oxyz, cho mặt cầu \((S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y-2z+5=0\). Phương trình mặt phẳng \((Q)\)chứa trục Ox và cắt \((S)\) theo giao tuyến là một đường tròn bán kính bằng 2 là
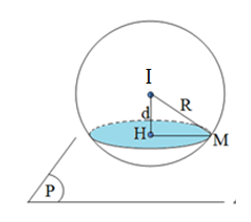
\((S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y-2z+5=0\Leftrightarrow {{(x-3)}^{2}}+{{(y+2)}^{2}}+{{(z-1)}^{2}}=9\)
\(\Rightarrow \left( S \right)\) có tâm \(I(3;-2;1)\), bán kính \(R=3\).
\((Q)\) cắt \((S)\) theo giao tuyến là một đường tròn bán kính \(r=2\)
Ta có: \({{d}^{2}}+{{r}^{2}}={{R}^{2}}\Leftrightarrow {{d}^{2}}+{{2}^{2}}={{3}^{2}}\Leftrightarrow d=\sqrt{5}\)
Gọi \(\overrightarrow{n}(a;b;c),\,\,\,\left( \overrightarrow{n}\ne \overrightarrow{0} \right)\) là một VTPT của (Q). Khi đó \(\overrightarrow{n}\) vuông góc với VTCP \(\overrightarrow{u}(1;0;0)\)của Ox \(\Rightarrow 1.a+0.b+0.c=0\Leftrightarrow a=0\)
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT \(\overrightarrow{n}(0;b;c),\,\,\,\left( \overrightarrow{n}\ne \overrightarrow{0} \right)\) là:
\(0.(x-0)+b(y-0)+c(z-0)=0\Leftrightarrow by+cz=0\)
Khoảng cách từ tâm I đến (Q):
\(d=\frac{\left| b.(-2)+c.1 \right|}{\sqrt{{{b}^{2}}+{{c}^{2}}}}=\sqrt{5}\Rightarrow {{\left( 2b-c \right)}^{2}}=5({{b}^{2}}+{{c}^{2}})\Leftrightarrow {{b}^{2}}+4bc+4{{c}^{2}}=0\Leftrightarrow {{(b+2c)}^{2}}=0\Leftrightarrow b=-2c\)
Cho \(c=-1\Rightarrow b=2\Rightarrow \overrightarrow{n}(0;2;-1)\). Phương trình mặt phẳng (Q): \(2y-z=0\).
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):x+y+z-1=0\), đường thẳng \(d:\frac{x-15}{1}=\frac{y-22}{2}=\frac{z-37}{2}\) và mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x-6y+4z+4=0\). Một đường thẳng \(\left( \Delta \right)\) thay đổi cắt mặt cầu \(\left( S \right)\) tại hai điểm \(A\), \(B\) sao cho \(AB=8\). Gọi \({A}'\), \({B}'\) là hai điểm lần lượt thuộc mặt phẳng \(\left( P \right)\) sao cho \(A{A}'\), \(B{B}'\) cùng song song với \(d\). Giá trị lớn nhất của biểu thức \(A{A}'+B{B}'\) là
Hình vẽ tham khảo
Mặt cầu \(\left( S \right)\) có tâm \(I\left( 4;3;-2 \right)\) và bán kính \(R=5\).
Gọi \(H\) là trung điểm của \(AB\) thì \(IH\bot AB\) và \(IH=3\) nên \(H\) thuộc mặt cầu \(\left( {{S}'} \right)\) tâm \(I\) bán kính \({R}'=3\).
Gọi \(M\) là trung điểm của \({A}'{B}'\) thì \(A{A}'+B{B}'=2HM\), \(M\) nằm trên mặt phẳng \(\left( P \right)\).
Mặt khác ta có \(d\left( I;\left( P \right) \right)=\frac{4}{\sqrt{3}}<R\) nên \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) và \(\sin \left( d;\left( P \right) \right)=\sin \alpha =\frac{5}{3\sqrt{3}}\). Gọi \(K\) là hình chiếu của \(H\) lên \(\left( P \right)\) thì \(HK=HM.\sin \alpha \). Vậy để \(A{A}'+B{B}'\) lớn nhất thì \(HK\) lớn nhất
\(\Leftrightarrow HK\) đi qua \(I\) nên \(H{{K}_{\max }}={R}'+d\left( I;\left( P \right) \right)=3+\frac{4}{\sqrt{3}}=\frac{4+3\sqrt{3}}{\sqrt{3}}\).
Vậy \(A{A}'+B{B}'\) lớn nhất bằng \(2\left( \frac{4+3\sqrt{3}}{\sqrt{3}} \right).\frac{3\sqrt{3}}{5}=\frac{24+18\sqrt{3}}{5}\).
Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-2 \right)}^{2}}=9\) và hai điểm \(M\left( 4;-\,4;2 \right),\,\,N\left( 6;0;6 \right).\) Gọi \(E\) là điểm thuộc mặt cầu \(\left( S \right)\) sao cho \(EM+EN\) đạt giá trị lớn nhất. Viết phương trình tiếp diện của mặt cầu \(\left( S \right)\) tại \(E.\)
Xét mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-2 \right)}^{2}}=9\) có tâm \(I\left( 1;2;2 \right),\) bán kính \(R=3.\)
Ta có \(MI=NI=3\sqrt{5}>3=R\)\(\Rightarrow \,\,M,\,\,N\) nằm bên ngoài khối cầu \(\left( S \right).\)
Gọi \(H\) là trung điểm của \(MN\)\(\Rightarrow \,\,H\left( 5;-\,2;4 \right)\) và \(E{{H}^{2}}=\frac{E{{M}^{2}}+E{{N}^{2}}}{2}-\frac{M{{N}^{2}}}{4}.\)
Lại có \({{\left( EM+EN \right)}^{2}}\le \left( {{1}^{2}}+{{1}^{2}} \right)\left( E{{M}^{2}}+E{{N}^{2}} \right)=2\left( E{{H}^{2}}+\frac{M{{N}^{2}}}{4} \right)\).
Để \({{\left\{ EM+EN \right\}}_{\max }}\Leftrightarrow E{{H}_{\max }}\)
Khi và chỉ khi \(E\) là giao điểm của \(IH\) và mặt cầu \(\left( S \right)\). Gọi \(\left( P \right)\) là mặt phẳng tiếp diện của \(\left( S \right)\) tại \(E\Rightarrow \,\,{{\vec{n}}_{\left( P \right)}}=a.\overrightarrow{EI}=b.\overrightarrow{IH}=b.\left( 4;-\,4;2 \right).\)
Dựa vào các đáp án ta thấy ở đáp án D, \({{\overrightarrow{n}}_{\left( P \right)}}=\left( 2;-2;1 \right)=\frac{1}{2}\left( 4;-4;2 \right)\)
Vậy phương trình mặt phẳng cần tìm là \(2x-2y+z+9=0.\)
Trong không gian Oxyz, cho mặt cầu \((S)\) có tâm là điểm \(I( - 1;2; - 3)\) và tiếp xúc với trục Ox. Phương trình của \((S)\) là
Bước 1: Gọi \(A\) là hình chiếu của \(I\) lên trục Ox. Tìm A và bán kính mặt cầu
Gọi \(A\) là hình chiếu của \(I\) lên trục \(Ox \Rightarrow A( - 1;0;0)\).
Vì điểm \(A\) nằm trên mặt cầu nên bán kính của mặt cầu là
\(R = IA = \sqrt {{0^2} + {{( - 2)}^2} + {{( - 3)}^2}} = \sqrt {13} \)
Bước 2: Viết phương trình mặt cầu
Phương trình mặt cầu \((S)\) tâm \(I( - 1;2; - 3)\) và bán kính \(R = \sqrt {13} \) là
\({(x + 1)^2} + {(y - 2)^2} + {(z + 3)^2} = 13\)

