Cho hàm số \(y = f(x)\) có đạo hàm \({f^\prime }(x) = {(x - 1)^2}\left( {{x^2} - 2x} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = f\left( {{x^2} - 8x + m} \right)\) có 5 điểm cực trị?
Bước 1: Giải \(f'\left( x \right) = 0\)
Ta có: \({f^\prime }(x) = {(x - 1)^2}\left( {{x^2} - 2x} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\\{x = 2}\end{array}} \right.\)
Bước 2: Xét hàm số \(g(x) = f\left( {{x^2} - 8x + m} \right)\). Giải \(g'\left( x \right) = 0\), biện luận nghiệm.
Đặt \(g(x) = f\left( {{x^2} - 8x + m} \right)\).
Ta có: \({g^\prime }(x) = (2x - 8){f^\prime }\left( {{x^2} - 8x + m} \right)\)
\(\begin{array}{l} \Rightarrow {g^\prime }(x) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 4}\\{{f^\prime }\left( {{x^2} - 8x + m} \right) = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 4}\\{{x^2} - 8x + m = 1(1)}\\{{x^2} - 8x + m = 0(2)}\\{{x^2} - 8x + m = 2(3)}\end{array}} \right.\end{array}\)
Để hàm số \(g(x)\) có 5 điểm cực trị thì \({g^\prime }(x) = 0\) có 5 nghiệm đơn phân biệt \( \Leftrightarrow \) phương trình \((2);(3)\) có 2 nghiệm phân biệt khác \(4\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{16 - m > 0}\\{18 - m > 0}\\{m - 16 \ne 0}\\{m - 18 \ne 0}\end{array} \Leftrightarrow m < 16} \right.\)
Vì \(m\) nguyên dương nên có 15 giá trị của \(m\) thỏa mãn.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 10} \right)\left( {{x^2} - 25} \right),\,\,\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {\left| {{x^3} + 8x} \right| + m} \right)\) có ít nhất 3 điểm cực trị?
* BBT của hàm số \(h\left( x \right) = \left| {{x^3} + 8x} \right|\):
* Xét \(g\left( x \right) = f\left( {\left| {{x^3} + 8x} \right| + m} \right)\) \( \Rightarrow g'\left( x \right) = \left( {\left| {{x^3} + 8x} \right|} \right)'.f'\left( {\left| {{x^3} + 8x} \right| + m} \right)\) \( = \left( {h\left( x \right)} \right)'.f'\left( {\left| {{x^3} + 8x} \right| + m} \right)\).
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}h'\left( x \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\f'\left( {\left| {{x^3} + 8x} \right| + m} \right) = 0\,\,\,\left( 2 \right)\end{array} \right.\)
+) Từ BBT của \(h\left( x \right)\) \( \Rightarrow h'\left( x \right) = 0\) chỉ chứa 1 nghiệm \(x = 0\) là điểm cực trị của \(h\left( x \right)\).
\( \Rightarrow \) Phương trình (1) \( \Leftrightarrow x = 0\) là nghiệm bội lẻ.
+) \(f'\left( x \right) = \left( {x - 10} \right)\left( {{x^2} - 25} \right) \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = - 5\\x = 5\end{array} \right.\).
\( \Rightarrow \) Phương trình (2) \( \Leftrightarrow \left[ \begin{array}{l}\left| {{x^3} + 8x} \right| + m = 10\\\left| {{x^3} + 8x} \right| + m = - 5\\\left| {{x^3} + 8x} \right| + m = 5\end{array} \right.\)
Để hàm số \(g\left( x \right)\) có ít nhất 3 điểm cực trị \( \Leftrightarrow \) ít nhất 1 trong 3 đường thẳng \(y = 10,\,\,y = 5,\,\,y = - 5\) phải cắt \(\left| {{x^3} + 5x} \right| + m\) tại 2 điểm phân biệt (2 nghiệm bội lẻ khác 0).
\( \Leftrightarrow m < 10 \Rightarrow \) Có tất cả 9 giá trị nguyên dương của \(m\) thỏa mãn yêu cầu bài toán.
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 9} \right)\left( {{x^2} - 16} \right),\,\forall x \in \mathbb{R}.\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {\left| {{x^3} + 7x} \right| + m} \right)\) có ít nhất \(3\) điểm cực trị?
Bảng biến thiên của \(h\left( x \right) = \left| {{x^3} + 7x} \right|\)
Xét \(g\left( x \right) = f\left( {\left| {{x^3} + 7x} \right| + m} \right)\). Ta có: \(g'\left( x \right) = \left( {\left| {{x^3} + 7x} \right|} \right)'.f'\left( {\left| {{x^3} + 7x} \right| + m} \right) = \left( {h\left( x \right)} \right)'.f'\left( {\left| {{x^3} + 7x} \right| + m} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}h'\left( x \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\f'\left( {\left| {{x^3} + 7x} \right| + m} \right) = 0\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ BBT của \(h\left( x \right) \Rightarrow h'\left( x \right) = 0\) chỉ chứa \(1\) nghiệm \(x = 0\) là điểm cực trị của \(h\left( x \right).\)
Do đó phương trình \(\left( 1 \right)\) có \(x = 0\) là nghiệm bội lẻ.
\(f'\left( x \right) = \left( {x - 9} \right)\left( {{x^2} - 16} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 9\\x = 4\\x = - 4\end{array} \right.\)
Phương trình \(\left( 2 \right)\) \( \Leftrightarrow \left[ \begin{array}{l}\left| {{x^3} + 7x} \right| + m = 9\\\left| {{x^3} + 7x} \right| + m = - 4\\\left| {{x^3} + 7x} \right| + m = 4\end{array} \right.\)
Ta có bảng biến thiên:
Để hàm số \(g\left( x \right)\) có ít nhất \(3\) điểm cực trị thì ít nhất \(1\) trong \(3\) đường thẳng \(y = 9,\,y = 4,\,y = - 4\) phải cắt \(\left( {\left| {{x^3} + 7x} \right| + m} \right)\) tại \(2\) điểm phân biệt (\(2\) nghiệm bội lẻ khác \(0\)).
\( \Leftrightarrow m < 9\). Có tất cả \(8\) giá trị nguyên dương \(m\) thỏa mãn.
Đề thi THPT QG - 2021 - mã 102
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 8} \right)\left( {{x^2} - 9} \right),\,\forall x \in \mathbb{R}.\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {\left| {{x^3} + 6x} \right| + m} \right)\) có ít nhất \(3\) điểm cực trị?
Bảng biến thiên của \(h\left( x \right) = \left| {{x^3} + 6x} \right|\)
Xét \(g\left( x \right) = f\left( {\left| {{x^3} + 6x} \right| + m} \right)\). Ta có: \(g'\left( x \right) = \left( {\left| {{x^3} + 6x} \right|} \right)'.f'\left( {\left| {{x^3} + 6x} \right| + m} \right) = \left( {h\left( x \right)} \right)'.f'\left( {\left| {{x^3} + 6x} \right| + m} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}h'\left( x \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\f'\left( {\left| {{x^3} + 6x} \right| + m} \right) = 0\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ BBT của \(h\left( x \right) \Rightarrow h'\left( x \right) = 0\) chỉ chứa \(1\) nghiệm \(x = 0\) là điểm cực trị của \(h\left( x \right).\)
Do đó phương trình \(\left( 1 \right)\) có \(x = 0\) là nghiệm bội lẻ.
\(f'\left( x \right) = \left( {x - 8} \right)\left( {{x^2} - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 8\\x = 3\\x = - 3\end{array} \right.\)
Phương trình \(\left( 2 \right)\) \( \Leftrightarrow \left[ \begin{array}{l}\left| {{x^3} + 6x} \right| + m = 8\\\left| {{x^3} + 6x} \right| + m = - 3\\\left| {{x^3} + 6x} \right| + m = 3\end{array} \right.\)
Ta có bảng biến thiên:
Để hàm số \(g\left( x \right)\) có ít nhất \(3\) điểm cực trị thì ít nhất \(1\) trong \(3\) đường thẳng \(y = 8,\,y = 3,\,y = - 3\) phải cắt \(\left( {\left| {{x^3} + 6x} \right| + m} \right)\) tại \(2\) điểm phân biệt (\(2\) nghiệm bội lẻ khác \(0\)).
\( \Leftrightarrow m < 8\). Có tất cả \(7\) giá trị \(m\) thỏa mãn.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 1} \right)^3}\left[ {{x^2} + \left( {4m - 5} \right)x + {m^2} - 7m + 6} \right],\,\,\forall x \in \mathbb{R}\). Có bao nhiêu số nguyên m để hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) có đúng 5 điểm cực trị?
Để hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) có đúng 5 điểm cực trị thì hàm số \(y = f\left( x \right)\) phải có 2 điểm cực trị dương \( \Rightarrow \) Phương trình \(f'\left( x \right) = 0\) phải có 2 nghiệm bội lẻ dương phân biệt.
Xét \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\left( {nghiem\,\,boi\,\,3} \right)\\{x^2} + \left( {4m - 5} \right)x + {m^2} - 7m + 6 = 0\,\,\left( * \right)\end{array} \right.\).
Do đó phương trình (*) cần phải có 1 nghiệm bội lẻ dương khác 1.
Ta có:
\(\begin{array}{l}\Delta = {\left( {4m - 5} \right)^2} - 4\left( {{m^2} - 7m + 6} \right)\\\,\,\,\,\, = 16{m^2} - 40m + 25 - 4{m^2} + 28m - 24\\\,\,\,\,\, = 12{m^2} - 12m + 1\end{array}\)
Để (*) có 1 nghiệm bội lẻ dương khác 1 thì:
\(\left\{ \begin{array}{l}\Delta = 12{m^2} - 12m + 1 > 0\\P = {m^2} - 7m + 6 \le 0\\1 + 4m - 5 + {m^2} - 7m + 6 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > \dfrac{{3 + \sqrt 6 }}{6}\\m < \dfrac{{3 - \sqrt 6 }}{6}\end{array} \right.\\1 \le m \le 6\\m \ne 1\\m \ne 2\end{array} \right.\) \(\Rightarrow \left\{ \begin{array}{l}1 < m \le 6\\m \ne 2\end{array} \right.\).
Vậy có 4 số nguyên m thỏa mãn yêu cầu bài toán.
Tìm giá trị nhỏ nhất của hàm số \(y = \left| {\sin x + \cos x + \tan x + \cot x + \dfrac{1}{{\sin x}} + \dfrac{1}{{\cos x}}} \right|\)
\(y = \left| {\sin x + \cos x + \tan x + \cot x + \dfrac{1}{{\sin x}} + \dfrac{1}{{\cos x}}} \right|\)
\(y = \left| {\sin x + \cos x + \dfrac{{1 + \sin x + \cos x}}{{\sin x\cos x}}} \right|\)
Đặt \(t = \sin x + \cos x\left( { - \sqrt 2 \le t \le \sqrt 2 } \right)\) thì \(\sin x\cos x = \dfrac{{{t^2} - 1}}{2}\)
Khi đó :
\(y = \left| {t + \dfrac{{2\left( {t + 1} \right)}}{{{t^2} - 1}}} \right| = \left| {t + \dfrac{2}{{t - 1}}} \right| = \left| {t - 1 + \dfrac{2}{{t - 1}} + 1} \right|\)
Nếu \(t - 1 > 0 \Rightarrow t - 1 + \dfrac{2}{{t - 1}} + 1 \ge 2\sqrt 2 + 1 \Rightarrow y \ge 2\sqrt 2 + 1\)
Nếu \(t - 1 < 0 \Leftrightarrow t < 1\) thì ta viết lại \(y = \left| {1 - t + \dfrac{2}{{1 - t}} - 1} \right|\)
Ta có: \(1 - t + \dfrac{2}{{1 - t}} \ge 2\sqrt 2 \) \( \Rightarrow 1 - t + \dfrac{2}{{1 - t}} - 1 \ge 2\sqrt 2 - 1\) hay \(y \ge 2\sqrt 2 - 1\)
Vậy \(y \ge 2\sqrt 2 - 1\)
Dấu bằng xảy ra \( \Leftrightarrow {\left( {1 - t} \right)^2} = 2 \Leftrightarrow t = 1 - \sqrt 2 \,\,\left( {t < 1} \right)\)
\( \Rightarrow \sin x + \cos x = 1 - \sqrt 2 \Leftrightarrow \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right) = 1 - \sqrt 2 \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) = \dfrac{{1 - \sqrt 2 }}{2}\)
Biết rằng đồ thị hàm số bậc 4: \(y = f\left( x \right)\) được cho như hình vẽ sau:
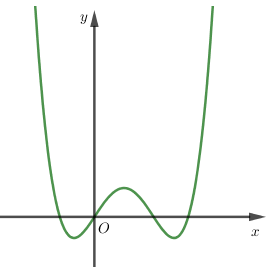
Tìm số giao điểm của đồ thị hàm số \(y = g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right)\) và trục $Ox.$
Đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại bốn điểm phân biệt nên \(f\left( x \right) = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right)\)
\( \Rightarrow f'\left( x \right) = a\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right)\) \( + a\left( {x - {x_1}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right)\) \( + a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_4}} \right)\) \( + a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\)
Rõ ràng \(f\left( x \right) = 0 \Rightarrow \left[ \begin{array}{l}x = {x_1}\\x = {x_2}\\x = {x_3}\\x = {x_4}\end{array} \right.\) \( \Rightarrow f'\left( x \right) \ne 0\) \( \Rightarrow g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f''\left( x \right).f\left( x \right) \ne 0\) nên ta chỉ xét \(f\left( x \right) \ne 0\)
\( \Rightarrow \dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = \dfrac{1}{{x - {x_1}}} + \dfrac{1}{{x - {x_2}}} + \dfrac{1}{{x - {x_3}}} + \dfrac{1}{{x - {x_4}}},\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}\)
Đặt \(h\left( x \right) = \dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = \dfrac{1}{{x - {x_1}}} + \dfrac{1}{{x - {x_2}}} + \dfrac{1}{{x - {x_3}}} + \dfrac{1}{{x - {x_4}}},\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}\)
Ta có $h'\left( x \right) = \dfrac{{f''\left( x \right).f\left( x \right) - {{\left[ {f'\left( x \right)} \right]}^2}}}{{{f^2}\left( x \right)}}$$ = \dfrac{{ - 1}}{{{{\left( {x - {x_1}} \right)}^2}}} + \dfrac{{ - 1}}{{{{\left( {x - {x_2}} \right)}^2}}} + \dfrac{{ - 1}}{{{{\left( {x - {x_3}} \right)}^2}}} + \dfrac{{ - 1}}{{{{\left( {x - {x_4}} \right)}^2}}} < 0,\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}$
$ \Rightarrow f''\left( x \right).f\left( x \right) - {\left[ {f'\left( x \right)} \right]^2} < 0,\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}$
$ \Rightarrow g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f''\left( x \right).f\left( x \right) > 0,\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}$
Vậy đồ thị hàm số \(y = g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right)\) không cắt trục $Ox.$
Với điều kiện \(\left\{ \begin{array}{l}ac\left( {{b^2} - 4ac} \right) > 0\\ab < 0\end{array} \right.\) thì đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) cắt trục hoành tại bao nhiêu điểm?
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) và đường thẳng $y = 0.$
Ta có: \(y' = 4a{x^3} + 2bx = 0 \Leftrightarrow 2x\left( {2a{x^2} + b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = - \dfrac{b}{{2a}}\end{array} \right.\)
Ta có \(ab < 0 \Rightarrow \) a, b trái dấu \( \Rightarrow - \dfrac{b}{{2a}} > 0 \Rightarrow \) phương trình $y' = 0$ có $3$ nghiệm phân biệt hay đồ thị hàm số có $3$ điểm cực trị.
+ Với \(x = 0 \Rightarrow y = c \Rightarrow A\left( {0;c} \right)\)
+ Với \({x^2} = - \dfrac{b}{{2a}} \Rightarrow x = \pm \sqrt { - \dfrac{b}{{2a}}} \) \( \Rightarrow y = \dfrac{{ - a\left( {{b^2} - 4ac} \right)}}{{4{a^2}}}\)
\( \Rightarrow B\left( { - \sqrt { - \dfrac{b}{{2a}}} ;\dfrac{{ - a\left( {{b^2} - 4ac} \right)}}{{4{a^2}}}} \right),C\left( {\sqrt { - \dfrac{b}{{2a}}} ;\dfrac{{ - a\left( {{b^2} - 4ac} \right)}}{{4{a^2}}}} \right)\)
Ta có \(ac\left( {{b^2} - 4ac} \right) > 0\) \( \Leftrightarrow \dfrac{{ - a\left( {{b^2} - 4ac} \right)}}{{4{a^2}}}.c < 0\) \( \Rightarrow {y_B}.{y_A} < 0\)
\( \Rightarrow \) Các điểm cực đại và cực tiểu nằm khác phía so với trục hoành
\( \Rightarrow \) Đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) cắt trục hoành tại \(4\) điểm phân biệt.
Cho hàm số $f(x) = {x^3} + a{x^2} + bx - 2$ thỏa mãn $\left\{ \begin{array}{l}a + b > 1\\3 + 2a + b < 0\end{array} \right.$. Số điểm cực trị của hàm số $y = \left| {f\left( {\left| x \right|} \right)} \right|$ bằng:
Ta có: $f(x) = {x^3} + a{x^2} + bx - 2$
$ + )f\left( 0 \right) = - 2 < 0;$ $f(1) = a + b - 1 > 0$ nên \(f\left( 0 \right).f\left( 1 \right) < 0\)
\( \Rightarrow \) phương trình \(f\left( x \right) = 0\) có ít nhất \(1\) nghiệm \({x_1} \in \left( {0;1} \right)\)
\( + )f\left( 2 \right) = 2\left( {3 + 2a + b} \right) < 0\) nên \(f\left( 1 \right).f\left( 2 \right) < 0\)
\( \Rightarrow \) phương trình \(f\left( x \right) = 0\) có ít nhất \(1\) nghiệm \({x_2} \in \left( {1;2} \right)\)
Do đó phương trình \(f\left( x \right) = 0\) có ít nhất hai nghiệm và đồ thị hàm số \(y = f\left( x \right)\) chỉ có thể có dạng:
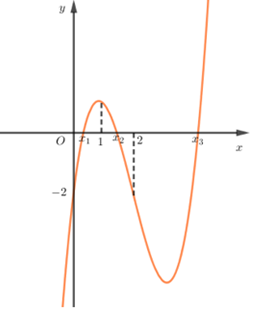
Khi đó, đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\)(màu tím) và \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) (màu cam) lần lượt có đồ thị như sau:
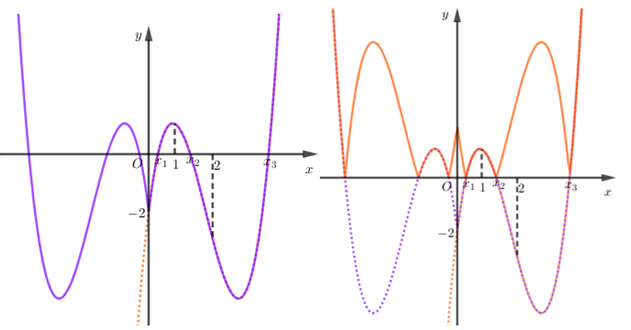
Như vậy, hàm số $y = \left| {f\left( {\left| x \right|} \right)} \right|$ có tất cả $11$ cực trị.
Cho hàm số $y = f(x)$ có đồ thị hàm số $f'(x)$ như hình vẽ. Hàm số $y = f(1 - x) + \dfrac{{{x^2}}}{2} - x$ nghịch biến trên khoảng
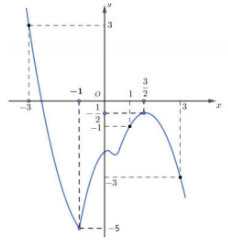
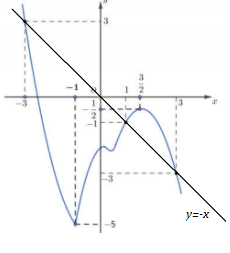
$y = f(1 - x) + \dfrac{{{x^2}}}{2} - x \Rightarrow y' = - f'(1 - x) + x - 1$
$\,y' < 0 \Leftrightarrow f'(1 - x) > - (1 - x)$
Dựa vào đồ thị hàm số, ta có: Đồ thị hàm số $f'(x)$ cắt đường thẳng $y = - x$ tại 3 điểm phân biệt là $A( - 3;3),\,\,B( - 1;1),\,\,C(3; - 3)$
$f'(1 - x) > - (1 - x) \Leftrightarrow \left[ \begin{array}{l}1 - x < - 3\\1 < 1 - x < 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 4\\ - 2 < x < 0\end{array} \right.$
Hàm số $y = f(1 - x) + \dfrac{{{x^2}}}{2} - x$ nghịch biến trên các khoảng $\left( { - 2;0} \right),\,\,\left( {4; + \infty } \right)$.
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = {x^8} + \left( {m - 2} \right){x^5} - \left( {{m^2} - 4} \right){x^4} + 1\) đạt cực tiểu tại \(x = 0\)?
Ta có \(y' = {x^3}\left[ {8{x^4} + 5x\left( {m - 2} \right) - 4\left( {{m^2} - 4} \right)} \right] = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\g\left( x \right) = 8{x^4} + 5x\left( {m - 2} \right) - 4\left( {{m^2} - 4} \right) = 0\end{array} \right.\)
Do \(x = 0\) là một nghiệm của đạo hàm nên hàm số đạt cực tiểu tại \(x = 0 \Leftrightarrow y'\) đổi dấu từ \( - \) sang \( + \) khi qua nghiệm \(x = 0\)
*) TH1: \(x = 0\) là nghiệm của \(g\left( x \right)\) hay \(m = \pm 2\)
Với $m{\rm{ }} = {\rm{ }}2$ thì $g\left( x \right) = 0$ có nghiệm $x = 0$ bội $4$ theo kết quả ở trên thì $x{\rm{ }} = {\rm{ }}0$ là nghiệm bội $7$ của $y'$ nên $x{\rm{ }} = {\rm{ }}0$ là điểm cực tiểu của hàm số nên chọn $m{\rm{ }} = {\rm{ }}2.$
Với $m = - 2$ thì $g\left( x \right)$ có nghiệm $x{\rm{ }} = {\rm{ }}0$ và 1 nghiệm dương, lúc này $x{\rm{ }} = {\rm{ }}0$ là nghiệm bội \(4\) của \(f'\left( x \right)\) nên \(x = 0\) không là điểm cực trị của hàm số. Loại $m{\rm{ }} = {\rm{ }} - {\rm{ }}2.$
*) TH2: \(x = 0\) không là nghiệm của \(g\left( x \right)\) hay $m \ne \pm 2$. Ta có \(g\left( 0 \right) = - 4\left( {{m^2} - 4} \right)\).
\(y' = {x^3}g\left( x \right)\) đổi dấu từ \( - \) sang \( + \) qua nghiệm \(x = 0\) khi và chỉ khi \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} g\left( x \right) > 0\\\mathop {\lim }\limits_{x \to {0^ - }} g\left( x \right) > 0\end{array} \right.\)
\( \Leftrightarrow - 4\left( {{m^2} - 4} \right) > 0\)\( \Leftrightarrow {m^2} - 4 < 0 \Leftrightarrow - 2 < m < 2\)
Do \(m\) nguyên nên \(m \in \left\{ { - 1;0;1} \right\}\)
Kết hợp hai trường hợp ta được \(m \in \left\{ { - 1;0;1;2} \right\}\)
Cho hàm số \(y = \dfrac{{x - 2}}{{x + 1}}\) có đồ thị \(\left( C \right).\) Gọi \(I\) là giao điểm của hai tiệm cận của \(\left( C \right).\) Xét tam giác đều \(ABI\) có hai đỉnh \(A,\;B\) thuộc \(\left( C \right),\) đoạn thẳng \(AB\) có độ dài bằng:
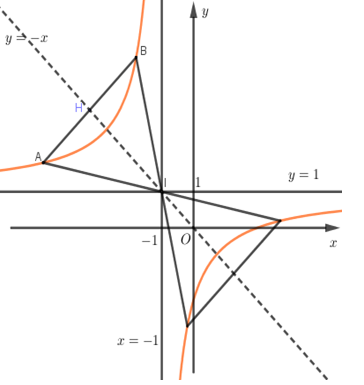
Ta có: \(x = - 1\) là TCĐ của đồ thị hàm số, \(y = 1\) là TCN của đồ thị hàm số.
\( \Rightarrow I\left( { - 1;\;1} \right)\) là giao điểm của hai đường tiệm cận của đồ thị hàm số.
Dựa vào đồ thị hàm số ta có \(\Delta IAB\) là tam giác đều
\( \Rightarrow IH\) vừa là đường cao đồng thời là đường phân giác của \(\angle AIB \Rightarrow IH\) cũng là đường phân giác của góc phần tư thứ hai.
\( \Rightarrow IH:\;\;y = - x.\)
Ta có: \(AB \bot IH \Rightarrow AB:\;\;y = x + m \Leftrightarrow x - y + m = 0.\)
\( \Rightarrow d\left( {I;\;AB} \right) = \dfrac{{\left| { - 1 - 1 + m} \right|}}{{\sqrt 2 }} = \dfrac{{\left| {m - 2} \right|}}{{\sqrt 2 }}.\)
Xét phương trình hoành độ giao điểm: \(\dfrac{{x - 2}}{{x + 1}} = x + m \Leftrightarrow {x^2} + mx + m + 2 = 0\)
Phương trình có hai nghiệm phân biệt \( \Leftrightarrow {m^2} - 4\left( {m + 2} \right) > 0 \Leftrightarrow {m^2} - 4m > 8\)
Khi đó hoành độ các giao điểm \(A,\;B\) là nghiệm của phương trình trên.
Gọi \(A\left( {{x_1};\;{x_1} + m} \right);B\left( {{x_2};\;{x_2} + m} \right)\)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - m\\{x_1}{x_2} = m + 2\end{array} \right..\)
\( \Rightarrow A{B^2} = {\left( {{x_1} - {x_2}} \right)^2} + {\left( {{x_1} + m - {x_2} - m} \right)^2}\) \( = 2{\left( {{x_1} - {x_2}} \right)^2} = 2{\left( {{x_1} + {x_2}} \right)^2} - 8{x_1}{x_2}\) \( = 2{m^2} - 8\left( {m + 2} \right)\)
Do tam giác \(IAB\) đều nên \(d\left( {I,AB} \right) = \dfrac{{AB\sqrt 3 }}{2}\) \( \Leftrightarrow {d^2}\left( {I,AB} \right) = \dfrac{{3A{B^2}}}{4}\)
\( \Leftrightarrow \dfrac{{{{\left( {m - 2} \right)}^2}}}{2} = \dfrac{{3\left[ {2{m^2} - 8\left( {m + 2} \right)} \right]}}{4}\) $ \Leftrightarrow {m^2} - 4m = 14$ (thỏa điều kiện \({m^2} - 4m > 8\))
$ \Rightarrow AB = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2}} $ $ = \sqrt {2{m^2} - 8\left( {m + 2} \right)} $ $ = \sqrt {2\left( {{m^2} - 4m - 8} \right)} $ \( = \sqrt {2.\left( {14 - 8} \right)} = \sqrt {12} = 2\sqrt 3 .\)
Cho hàm số \(y = \dfrac{1}{6}{x^4} - \dfrac{7}{3}{x^2}\) có đồ thị hàm số \(\left( C \right).\) Có bao nhiêu điểm \(A\) thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(A\) cắt \(\left( C \right)\) tại hai điểm phân biệt \(M\left( {{x_1};\;{y_1}} \right),\;N\left( {{x_2};\;{y_2}} \right)\;\;\left( {M,\;N \ne A} \right)\) thỏa mãn \({y_1} - {y_2} = 4\left( {{x_1} - {x_2}} \right)?\)
Gọi \(A\left( {{x_0};\;{y_0}} \right) \in \left( C \right).\)
Khi đó tiếp tuyến của \(\left( C \right)\) tại $A$ cắt \(\left( C \right)\) tại hai điểm phân biệt \(M\left( {{x_1};\;{y_1}} \right),\;N\left( {{x_2};\;{y_2}} \right)\;\;\left( {M,\;N \ne A} \right)\) có hệ số góc là: \(k = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}} = 4.\)
Mặt khác: \(k = f'\left( {{x_0}} \right) \Rightarrow 4 = \dfrac{2}{3}{x^3} - \dfrac{{14}}{3}x \Leftrightarrow x_0^3 - 7{x_0} - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} = - 2\\{x_0} = - 1\\{x_0} = 3\end{array} \right..\)
Kiểm tra lại từng trường hợp $x_0=-2;-1;3$ ta thấy trường hợp $x_0=3$ thì tiếp tuyến chỉ có duy nhất $1$ điểm chung với đồ thị nên loại.
Vậy có $2$ giá trị của \(m\) thỏa mãn.
Cho hai hàm số \(y = f\left( x \right),\;y = g\left( x \right).\) Hai hàm số \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị hàm như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right).\) Hàm số \(h\left( x \right) = f\left( {x + 6} \right) - g\left( {2x + \dfrac{5}{2}} \right)\) đồng biến trên khoảng nào dưới đây?
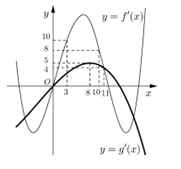
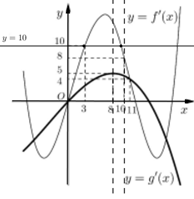
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 10\) cắt đồ thị hàm số \(y = f'\left( x \right)\) tại hai điểm phân biệt \(\left( {3;\;10} \right)\) và \(\left( {m;\;10} \right)\) với mọi \(m \in \left( {8;\;10} \right).\)
Ta có:
$f'\left( {x + 6} \right) \ge 10 \Leftrightarrow 3 \le x + 6 \le m < 10$ $ \Rightarrow - 3 \le x < 4$
$g'\left( {2x + \frac{5}{2}} \right) \le 5,\forall x \in R$
$\Rightarrow h'\left( x \right) = f'\left( {x + 6} \right) - 2g'\left( {2x + \frac{5}{2}} \right) $$\ge 10-2.5=0,\forall x \in \left[ { - 3;4} \right)$
Do đó hàm số h(x) đồng biến trên [-3;4)
Dựa vào các đáp án ta thấy đáp án B thỏa mãn.
Cho hàm số \(f\left( x \right) = {x^3} - 6{x^2} + 9x\). Đặt \({f^k}\left( x \right) = f\left( {{f^{k - 1}}\left( x \right)} \right)\) (với $k$ là số tự nhiên lớn hơn $1$). Tính số nghiệm của phương trình \({f^8}\left( x \right) = 0\)
Ta có đồ thị hàm số \(f\left( x \right) = {x^3} - 6{x^2} + 9x\) như sau:
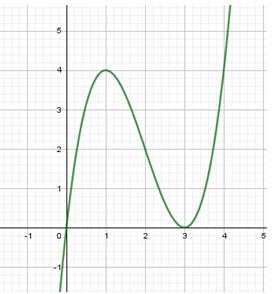
Dựa vào đồ thị hàm số ta có thể suy ra số nghiệm của phương trình \(f\left( x \right) = m\) như sau:
\(\left[ \begin{array}{l}m < 0\\m > 4\end{array} \right. \Rightarrow \) phương trình có $1$ nghiệm duy nhất.
\(\left[ \begin{array}{l}m = 0\\m = 4\end{array} \right. \Rightarrow \) phương trình có $2$ nghiệm phân biệt.
\(0 < m < 4 \Rightarrow \) phương trình có $3$ nghiệm phân biệt.
Xét phương trình \({f^2}\left( x \right) = 0 \Leftrightarrow {\left( {f\left( x \right)} \right)^3} - 6{\left( {f\left( x \right)} \right)^2} + 9f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f\left( x \right) = 3\end{array} \right.\)
Ta thấy phương trình \(f\left( x \right) = 0\) có $2$ nghiệm phân biệt, phương trình \(f\left( x \right) = 3\) có $3$ nghiệm phân biệt.
Vậy phương trình \({f^2}\left( x \right) = 0\) có $5$ nghiệm phân biệt
Xét phương trình \({f^3}\left( x \right) = 0 \Leftrightarrow f\left( {{f^2}\left( x \right)} \right) = 0 \Leftrightarrow {\left( {{f^2}\left( x \right)} \right)^3} - 6{\left( {{f^2}\left( x \right)} \right)^2} + 9{f^2}\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{f^2}\left( x \right) = 0\\{f^2}\left( x \right) = 3\end{array} \right.\)
Phương trình \({f^2}\left( x \right) = 0\) có $2 + 3 $ nghiệm phân biệt.
Phương trình \({f^2}\left( x \right) = 3 \Leftrightarrow {\left( {f\left( x \right)} \right)^3} - 6{\left( {f\left( x \right)} \right)^2} + 9f\left( x \right) = 3 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) \approx 3,88 \in \left( {0;4} \right)\\f\left( x \right) \approx 1,65 \in \left( {0;4} \right)\\f\left( x \right) \approx 0,46 \in \left( {0;4} \right)\end{array} \right.\)
\( \Rightarrow \) phương trình \({f^2}\left( x \right) = 3\) có $9$ nghiệm phân biệt.
Vậy phương trình \({f^3}\left( x \right) = 0\) có \(2 + 3 + {3^2}\) nghiệm phân biệt.
Xét phương trình \({f^4}\left( x \right) = 0 \Leftrightarrow f\left( {{f^3}\left( x \right)} \right) = 0 \Leftrightarrow {\left( {{f^3}\left( x \right)} \right)^3} - 6{\left( {{f^3}\left( x \right)} \right)^2} + 9{f^3}\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{f^3}\left( x \right) = 0\\{f^3}\left( x \right) = 3\end{array} \right.\)
Phương trình \({f^3}\left( x \right) = 0\) có \(2 + 3 + {3^2}\) nghiệm phân biệt (cmt).
Phương trình
\({f^3}\left( x \right) = 3 \Leftrightarrow {\left( {{f^2}\left( x \right)} \right)^3} - 6{\left( {{f^2}\left( x \right)} \right)^2} + 9{f^2}\left( x \right) = 3 \Leftrightarrow \left[ \begin{array}{l}{f^2}\left( x \right) \approx 3,88 \in \left( {0;4} \right)\\{f^2}\left( x \right) \approx 1,65 \in \left( {0;4} \right)\\{f^2}\left( x \right) \approx 0,46 \in \left( {0;4} \right)\end{array} \right.\)
Ta thấy mỗi phương trình $f^2(x)=m$ ở trên có $9$ nghiệm phân biệt nên $3$ phương trình sẽ có $3.9=3^3$ nghiệm phân biệt.
Vậy phương trình \({f^4}\left( x \right) = 0\) có \(2 + 3 + {3^2} + {3^3}\) nghiệm.
Cứ như vậy ta tính được phương trình \({f^8}\left( x \right) = 0\) có \(2 + 3 + {3^2} + {3^3} + ... + {3^7} = 2 + \dfrac{{3\left( {1 - {3^7}} \right)}}{{1 - 3}} = 3281\) nghiệm.
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 7} \right)\left( {{x^2} - 9} \right),\,\forall \,x \in \,\mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {\left| {{x^3} + 5x} \right| + m} \right)\) có ít nhất 3 điểm cực trị?
* BBT của hàm số \(h\left( x \right) = \left| {{x^3} + 5x} \right|\):
* Xét \(g\left( x \right) = f\left( {\left| {{x^3} + 5x} \right| + m} \right)\) \( \Rightarrow g'\left( x \right) = \left( {\left| {{x^3} + 5x} \right|} \right)'.f'\left( {\left| {{x^3} + 5x} \right| + m} \right)\) \( = \left( {h\left( x \right)} \right)'.f'\left( {\left| {{x^3} + 5x} \right| + m} \right)\).
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}h'\left( x \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\f'\left( {\left| {{x^3} + 5x} \right| + m} \right) = 0\,\,\,\left( 2 \right)\end{array} \right.\)
+) Từ BBT của \(h\left( x \right)\) \( \Rightarrow h'\left( x \right) = 0\) chỉ chứa 1 nghiệm \(x = 0\) là điểm cực trị của \(h\left( x \right)\).
\( \Rightarrow \) Phương trình (1) \( \Leftrightarrow x = 0\) là nghiệm bội lẻ.
+) \(f'\left( x \right) = \left( {x - 7} \right)\left( {{x^2} - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 7\\x = - 3\\x = 3\end{array} \right.\).
\( \Rightarrow \) Phương trình (2) \( \Leftrightarrow \left[ \begin{array}{l}\left| {{x^3} + 5x} \right| + m = 7\\\left| {{x^3} + 5x} \right| + m = - 3\\\left| {{x^3} + 5x} \right| + m = 3\end{array} \right.\)
Để hàm số \(g\left( x \right)\) có ít nhất 3 điểm cực trị \( \Leftrightarrow \) ít nhất 1 trong 3 đường thẳng \(y = 7,\,\,y = 3,\,\,y = - 3\) phải cắt \(\left| {{x^3} + 5x} \right| + m\) tại 2 điểm phân biệt (2 nghiệm bội lẻ khác 0).
\( \Leftrightarrow m < 7 \Rightarrow \) Có tất cả 6 giá trị nguyên dương của \(m\) thỏa mãn yêu cầu bài toán.
Theo thống kê tại một nhà máy \(Z\), nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P(x) = \dfrac{{95{x^2} + 120x}}{4}\), với \(x\) là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần mấy giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?
\(x = 36\).
\(x = 36\).
\(x = 36\).
Bước 1: Gọi \(t\) là số giờ làm tăng thêm mỗi tuần, \(t \in \mathbb{R}\). Biểu diễn các đại lượng khác theo t.
Gọi \(t\) là số giờ làm tăng thêm mỗi tuần, \(t \in \mathbb{R}\) \( \Rightarrow \) số công nhân bỏ việc là \(\dfrac{t}{2}\) nên số công nhân làm việc là \(100 - \dfrac{t}{2}\) người.
Năng suất của công nhân còn \(120 - \dfrac{{5t}}{2}\) sản phẩm một giờ.
Số thời gian làm việc một tuần là \(40 + t = x\) giờ.
Bước 2: Lập hệ bất phương trình và tìm điều kiện của t.
Để nhà máy hoạt động được thì \(\left\{ {\begin{array}{*{20}{l}}{40 + t > 0}\\{120 - \dfrac{{5t}}{2} > 0 \Rightarrow t \in ( - 40;48)}\\{100 - \dfrac{t}{2} > 0}\end{array}} \right.\)
Bước 3: Biểu diễn số sản phẩm thu được theo t và khảo sát hàm số f(t).
Số sản phẩm trong một tuần làm được: \(S = \left( {100 - \dfrac{t}{2}} \right)\left( {120 - \dfrac{{5t}}{2}} \right)(40 + t)\).
Số sản phẩm thu được là
\(f(t) = \left( {100 - \dfrac{t}{2}} \right)\left( {120 - \dfrac{{5t}}{2}} \right)(40 + t) - \dfrac{{95{{(40 + t)}^2} + 120(40 + t)}}{4}\).
\({f^\prime }(t) = \)\( - \dfrac{1}{2}\left( {120 - \dfrac{{5t}}{2}} \right)(40 + t)\)\( - \dfrac{5}{2}\left( {100 - \dfrac{t}{2}} \right)(40 + t)\)\( + \left( {100 - \dfrac{t}{2}} \right)\left( {120 - \dfrac{{5t}}{2}} \right)\)\( - \dfrac{{95}}{2}(40 + t) - 30 = \)\(\dfrac{{15}}{4}{t^2} - \dfrac{{1135}}{2}t - 2330\)
Ta có \({f^\prime }(t) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = - 4}\\{t = \dfrac{{466}}{3}(\;{\rm{L}})}\end{array}} \right.\).
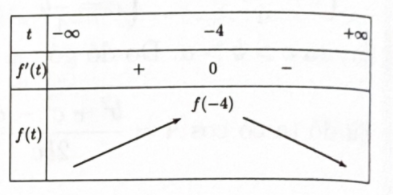
Bước 4: Tìm \(maxf\left( t \right)\) rồi tìm x.
Dựa vào bảng biến thiên ta có số lượng sản phẩm thu được mỗi tuần lớn nhất khi \(t = - 4 \Rightarrow x = 36\)

