Cho hàm số \(y = \dfrac{{x - 2}}{{x + 1}}\) có đồ thị \(\left( C \right).\) Gọi \(I\) là giao điểm của hai tiệm cận của \(\left( C \right).\) Xét tam giác đều \(ABI\) có hai đỉnh \(A,\;B\) thuộc \(\left( C \right),\) đoạn thẳng \(AB\) có độ dài bằng:

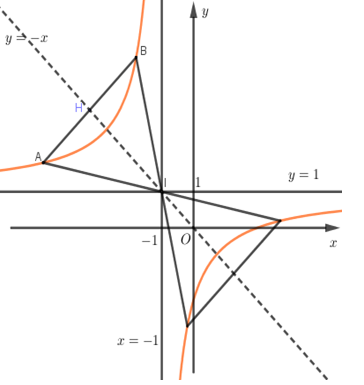
Ta có: \(x =  - 1\) là TCĐ của đồ thị hàm số, \(y = 1\) là TCN của đồ thị hàm số.

\( \Rightarrow I\left( { - 1;\;1} \right)\) là giao điểm của hai đường tiệm cận của đồ thị hàm số.

Dựa vào đồ thị hàm số ta có \(\Delta IAB\) là tam giác đều

\( \Rightarrow IH\) vừa là đường cao đồng thời là đường phân giác của \(\angle AIB \Rightarrow IH\) cũng là đường phân giác của góc phần tư thứ hai.

\( \Rightarrow IH:\;\;y =  - x.\)

Ta có: \(AB \bot IH \Rightarrow AB:\;\;y = x + m \Leftrightarrow x - y + m = 0.\)

\( \Rightarrow d\left( {I;\;AB} \right) = \dfrac{{\left| { - 1 - 1 + m} \right|}}{{\sqrt 2 }} = \dfrac{{\left| {m - 2} \right|}}{{\sqrt 2 }}.\)

Xét phương trình hoành độ giao điểm: \(\dfrac{{x - 2}}{{x + 1}} = x + m \Leftrightarrow {x^2} + mx + m + 2 = 0\)

Phương trình có hai nghiệm phân biệt \( \Leftrightarrow {m^2} - 4\left( {m + 2} \right) > 0 \Leftrightarrow {m^2} - 4m > 8\)

Khi đó hoành độ các giao điểm \(A,\;B\) là nghiệm của phương trình trên.

Gọi \(A\left( {{x_1};\;{x_1} + m} \right);B\left( {{x_2};\;{x_2} + m} \right)\)

Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - m\\{x_1}{x_2} = m + 2\end{array} \right..\)

\( \Rightarrow A{B^2} = {\left( {{x_1} - {x_2}} \right)^2} + {\left( {{x_1} + m - {x_2} - m} \right)^2}\) \( = 2{\left( {{x_1} - {x_2}} \right)^2} = 2{\left( {{x_1} + {x_2}} \right)^2} - 8{x_1}{x_2}\) \( = 2{m^2} - 8\left( {m + 2} \right)\)

Do tam giác \(IAB\) đều nên \(d\left( {I,AB} \right) = \dfrac{{AB\sqrt 3 }}{2}\) \( \Leftrightarrow {d^2}\left( {I,AB} \right) = \dfrac{{3A{B^2}}}{4}\)

\( \Leftrightarrow \dfrac{{{{\left( {m - 2} \right)}^2}}}{2} = \dfrac{{3\left[ {2{m^2} - 8\left( {m + 2} \right)} \right]}}{4}\) $ \Leftrightarrow {m^2} - 4m = 14$ (thỏa điều kiện \({m^2} - 4m > 8\))

$ \Rightarrow AB = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2}} $ $ = \sqrt {2{m^2} - 8\left( {m + 2} \right)} $ $ = \sqrt {2\left( {{m^2} - 4m - 8} \right)} $ \( = \sqrt {2.\left( {14 - 8} \right)}  = \sqrt {12}  = 2\sqrt 3 .\)